Chapter 6. Operations on Objects

This chapter describes the operations on objects, including lists, numbers, characters, strings, vectors, and symbols. The first section covers constant objects and quotation. The second section describes generic equivalence predicates for comparing two objects and predicates for determining the type of an object. Later sections describe procedures that deal primarily with one of the object types mentioned above. There is no section treating operations on procedures, since the only operation defined specifically for procedures is application, and this is described in Chapter 5. Operations on ports are covered in the more general discussion of input and output in Chapter 7.

Section 6.1. Constants and Quotation

syntax: constant
returns: constant

constant is any self-evaluating constant, i.e., a number, boolean, character, or string. Constants are immutable; see the note in the description of quote below.

3.2  3.2
#f  #f
#\c  #\c
"hi"  "hi"

syntax: (quote obj)
syntax: 'obj
returns: obj

'obj is equivalent to (quote obj). The abbreviated form is converted into the longer form by the Scheme reader (see read).

quote inhibits the normal evaluation rule for obj, allowing obj to be employed as data. Although any Scheme object may be quoted, quotation is not necessary for self-evaluating constants, i.e., numbers, booleans, characters, and strings.

Quoted and self-evaluating constants are immutable. That is, it is an error to alter a constant via set-car!, string-set!, etc. An implementation may choose to share storage among different constants to save space.

(+ 2 3)  5
'(+ 2 3)  (+ 2 3)
(quote (+ 2 3))  (+ 2 3)
'a  a
'cons  cons
'()  ()
'7  7

syntax: (quasiquote obj)
syntax: `obj
syntax: (unquote obj)
syntax: ,obj
syntax: (unquote-splicing obj)
syntax: ,@obj
returns: see explanation

`obj is equivalent to (quasiquote obj), ,obj is equivalent to (unquote obj), and ,@obj is equivalent to (unquote-splicing obj). The abbreviated forms are converted into the longer forms by the Scheme reader (see read).

quasiquote is similar to quote, but it allows parts of the quoted text to be "unquoted." Within a quasiquote expression, subforms of unquote and unquote-splicing forms are evaluated, and everything else is quoted, i.e., left unevaluated. The value of each unquote subform is inserted into the output in place of the unquote form, while the value of each unquote-splicing subform is spliced into the surrounding list or vector structure. unquote and unquote-splicing are valid only within quasiquote expressions.

quasiquote expressions may be nested, with each quasiquote introducing a new level of quotation and each unquote or unquote-splicing taking away a level of quotation. An expression nested within n quasiquote expressions must be within n unquote or unquote-splicing expressions to be evaluated.

`(+ 2 3)  (+ 2 3)

`(+ 2 ,(* 3 4))  (+ 2 12)
`(a b (,(+ 2 3) c) d)  (a b (5 c) d)
`(a b ,(reverse '(c d e)) f g)  (a b (e d c) f g)
(let ((a 1) (b 2))
  `(,a . ,b))  (1 . 2)

`(+ ,@(cdr '(* 2 3)))  (+ 2 3)
`(a b ,@(reverse '(c d e)) f g)  (a b e d c f g)
(let ((a 1) (b 2))
  `(,a ,@b))  (1 . 2)
`#(,@(list 1 2 3))  #(1 2 3)

'`,(cons 'a 'b)  `,(cons 'a 'b)
`',(cons 'a 'b)  '(a . b)

Section 6.2. Generic Equivalence and Type Predicates

This section describes the basic Scheme predicates (procedures returning one of the boolean values #t or #f) for determining the type of an object or the equivalence of two objects. The equivalence predicates eq?, eqv?, and equal? are discussed first, followed by the type predicates.

procedure: (eq? obj₁ obj₂)
returns: #t if obj₁ and obj₂ are identical, #f otherwise

In most Scheme systems, two objects are considered identical if they are represented internally by the same pointer value and distinct (not identical) if they are represented internally by different pointer values, although other criteria, such as time-stamping, are possible.

Although the particular rules for object identity vary somewhat from system to system, the following rules always hold.

• Two objects of different types (booleans, the empty list, pairs, numbers, characters, strings, vectors, symbols, and procedures) are distinct.

• Two objects of the same type with different contents or values are distinct.

• The boolean object #t is identical to itself wherever it appears, and #f is identical to itself wherever it appears, but #t and #f are distinct.

• The empty list () is identical to itself wherever it appears.

• Two symbols (created by read or by string->symbol) are identical if and only if they have the same name (by string=?).

• A quoted pair, vector, or string is identical to itself, as is a pair, vector, or string created by an application of cons, vector, string, etc. Two pairs, vectors, or strings created by different applications of cons, vector, string, etc., are distinct. One consequence is that cons, for example, may be used to create a unique object distinct from all other objects.

• Two procedures that may behave differently are distinct. A procedure created by an evaluation of a lambda expression is identical to itself. Two procedures created by the same lambda expression at different times, or by similar lambda expressions, may or may not be identical.

eq? cannot be used to compare numbers and characters reliably. Although every inexact number is distinct from every exact number, two exact numbers, two inexact numbers, or two characters with the same value may or may not be identical.

Since constant objects are immutable, i.e., it is an error to modify one, all or portions of different quoted constants or self-evaluating literals may be represented internally by the same object. Thus, eq? may return #t when applied to equal parts of different immutable constants.

(eq? 'a 3)  #f
(eq? #t 't)  #f
(eq? "abc" 'abc)  #f
(eq? "hi" '(hi))  #f
(eq? #f '())  #f

(eq? 9/2 7/2)  #f
(eq? 3.4 53344)  #f
(eq? 3 3.0)  #f
(eq? 1/3 #i1/3)  #f

(eq? 9/2 9/2)  unspecified
(eq? 3.4 (+ 3.0 .4))  unspecified
(let ((x (* 12345678987654321 2)))
  (eq? x x))  unspecified

(eq? #\a #\b)  #f
(eq? #\a #\a)  unspecified
(let ((x (string-ref "hi" 0)))
  (eq? x x))  unspecified

(eq? #t #t)  #t
(eq? #f #f)  #t
(eq? #t #f)  #f
(eq? (null? '()) #t)  #t
(eq? (null? '(a)) #f)  #t

(eq? (cdr '(a)) '())  #t

(eq? 'a 'a)  #t
(eq? 'a 'b)  #f
(eq? 'a (string->symbol "a"))  #t

(eq? '(a) '(b))  #f
(eq? '(a) '(a))  unspecified
(let ((x '(a . b))) (eq? x x))  #t
(let ((x (cons 'a 'b)))
  (eq? x x))  #t
(eq? (cons 'a 'b) (cons 'a 'b))  #f

(eq? "abc" "cba")  #f
(eq? "abc" "abc")  unspecified
(let ((x "hi")) (eq? x x))  #t
(let ((x (string #\h #\i))) (eq? x x))  #t
(eq? (string #\h #\i)
     (string #\h #\i))  #f

(eq? '#(a) '#(b))  #f
(eq? '#(a) '#(a))  unspecified
(let ((x '#(a))) (eq? x x))  #t
(let ((x (vector 'a)))
  (eq? x x))  #t
(eq? (vector 'a) (vector 'a))  #f

(eq? car car)  #t
(eq? car cdr)  #f
(let ((f (lambda (x) x)))
  (eq? f f))  #t
(let ((f (lambda () (lambda (x) x))))
  (eq? (f) (f)))  unspecified
(eq? (lambda (x) x) (lambda (y) y))  unspecified

(let ((f (lambda (x)
           (lambda ()
             (set! x (+ x 1))
             x))))
  (eq? (f 0) (f 0)))  #f

procedure: (eqv? obj₁ obj₂)
returns: #t if obj₁ and obj₂ are equivalent, #f otherwise

eqv? is similar to eq? except that eqv? is guaranteed to return #t for two exact numbers, two inexact numbers, or two characters with the same value (by = or char=?). eqv? is less implementation-dependent but generally more expensive than eq?. eqv? might be defined as follows.

(define eqv?
  (lambda (x y)
    (cond
      ((eq? x y))
      ((number? x)
       (and (number? y)
            (if (exact? x)
                (and (exact? y) (= x y))
                (and (inexact? y) (= x y)))))
      ((char? x) (and (char? y) (char=? x y)))
      (else #f))))

(eqv? 'a 3)  #f
(eqv? #t 't)  #f
(eqv? "abc" 'abc)  #f
(eqv? "hi" '(hi))  #f
(eqv? #f '())  #f

(eqv? 9/2 7/2)  #f
(eqv? 3.4 53344)  #f
(eqv? 3 3.0)  #f
(eqv? 1/3 #i1/3)  #f

(eqv? 9/2 9/2)  #t
(eqv? 3.4 (+ 3.0 .4))  #t
(let ((x (* 12345678987654321 2)))
  (eqv? x x))  #t

(eqv? #\a #\b)  #f
(eqv? #\a #\a)  #t
(let ((x (string-ref "hi" 0)))
  (eqv? x x))  #t

(eqv? #t #t)  #t
(eqv? #f #f)  #t
(eqv? #t #f)  #f
(eqv? (null? '()) #t)  #t
(eqv? (null? '(a)) #f)  #t

(eqv? (cdr '(a)) '())  #t

(eqv? 'a 'a)  #t
(eqv? 'a 'b)  #f
(eqv? 'a (string->symbol "a"))  #t

(eqv? '(a) '(b))  #f
(eqv? '(a) '(a))  unspecified
(let ((x '(a . b))) (eqv? x x))  #t
(let ((x (cons 'a 'b)))
  (eqv? x x))  #t
(eqv? (cons 'a 'b) (cons 'a 'b))  #f

(eqv? "abc" "cba")  #f
(eqv? "abc" "abc")  unspecified
(let ((x "hi")) (eqv? x x))  #t
(let ((x (string #\h #\i))) (eqv? x x))  #t
(eqv? (string #\h #\i)
      (string #\h #\i))  #f

(eqv? '#(a) '#(b))  #f
(eqv? '#(a) '#(a))  unspecified
(let ((x '#(a))) (eqv? x x))  #t
(let ((x (vector 'a)))
  (eqv? x x))  #t
(eqv? (vector 'a) (vector 'a))  #f

(eqv? car car)  #t
(eqv? car cdr)  #f
(let ((f (lambda (x) x)))
  (eqv? f f))  #t
(let ((f (lambda () (lambda (x) x))))
  (eqv? (f) (f)))  unspecified
(eqv? (lambda (x) x) (lambda (y) y))  unspecified

(let ((f (lambda (x)
           (lambda ()
             (set! x (+ x 1))
             x))))
  (eqv? (f 0) (f 0)))  #f

procedure: (equal? obj₁ obj₂)
returns: #t if obj₁ and obj₂ have the same structure and contents, #f otherwise

Two objects are equal if they are equivalent according to eqv? or if they are strings that are string=?, pairs whose cars and cdrs are equal, or vectors of the same length whose corresponding elements are equal.

equal? is recursively defined and must compare not only numbers and characters for equivalence but also pairs, strings, and vectors. The result is that equal? is less discriminating than either eq? or eqv?. It is also likely to be more expensive.

equal? might be defined as follows.

(define equal?
  (lambda (x y)
    (cond
      ((eqv? x y))
      ((pair? x)
       (and (pair? y)
            (equal? (car x) (car y))
            (equal? (cdr x) (cdr y))))
      ((string? x) (and (string? y) (string=? x y)))
      ((vector? x)
       (and (vector? y)
            (let ((n (vector-length x)))
              (and (= (vector-length y) n)
                   (let loop ((i 0))
                     (or (= i n)
                         (and (equal? (vector-ref x i) (vector-ref y i))
                              (loop (+ i 1)))))))))
      (else #f))))

(equal? 'a 3)  #f
(equal? #t 't)  #f
(equal? "abc" 'abc)  #f
(equal? "hi" '(hi))  #f
(equal? #f '())  #f

(equal? 9/2 7/2)  #f
(equal? 3.4 53344)  #f
(equal? 3 3.0)  #f
(equal? 1/3 #i1/3)  #f

(equal? 9/2 9/2)  #t
(equal? 3.4 (+ 3.0 .4))  #t
(let ((x (* 12345678987654321 2)))
  (equal? x x))  #t

(equal? #\a #\b)  #f
(equal? #\a #\a)  #t
(let ((x (string-ref "hi" 0)))
  (equal? x x))  #t

(equal? #t #t)  #t
(equal? #f #f)  #t
(equal? #t #f)  #f
(equal? (null? '()) #t)  #t
(equal? (null? '(a)) #f)  #t

(equal? (cdr '(a)) '())  #t

(equal? 'a 'a)  #t
(equal? 'a 'b)  #f
(equal? 'a (string->symbol "a"))  #t

(equal? '(a) '(b))  #f
(equal? '(a) '(a))  #t
(let ((x '(a . b))) (equal? x x))  #t
(let ((x (cons 'a 'b)))
  (equal? x x))  #t
(equal? (cons 'a 'b) (cons 'a 'b))  #t

(equal? "abc" "cba")  #f
(equal? "abc" "abc")  #t
(let ((x "hi")) (equal? x x))  #t
(let ((x (string #\h #\i))) (equal? x x))  #t
(equal? (string #\h #\i)
        (string #\h #\i))  #t

(equal? '#(a) '#(b))  #f
(equal? '#(a) '#(a))  #t
(let ((x '#(a))) (equal? x x))  #t
(let ((x (vector 'a)))
  (equal? x x))  #t
(equal? (vector 'a) (vector 'a))  #t

(equal? car car)  #t
(equal? car cdr)  #f
(let ((f (lambda (x) x)))
  (equal? f f))  #t
(let ((f (lambda () (lambda (x) x))))
  (equal? (f) (f)))  unspecified
(equal? (lambda (x) x) (lambda (y) y))  unspecified

(let ((f (lambda (x)
           (lambda ()
             (set! x (+ x 1))
             x))))
  (equal? (f 0) (f 0)))  #f

procedure: (boolean? obj)
returns: #t if obj is either #t or #f, #f otherwise

boolean? is equivalent to (lambda (x) (or (eq? x #t) (eq? x #f))).

(boolean? #t)  #t
(boolean? #f)  #t
(boolean? 't)  #f
(boolean? '())  #f

procedure: (null? obj)
returns: #t if obj is the empty list, #f otherwise

null? is equivalent to (lambda (x) (eq? x '())).

(null? '())  #t
(null? '(a))  #f
(null? (cdr '(a)))  #t
(null? 3)  #f
(null? #f)  #f

procedure: (pair? obj)
returns: #t if obj is a pair, #f otherwise

(pair? '(a b c))  #t
(pair? '(3 . 4))  #t
(pair? '())  #f
(pair? '#(a b))  #f
(pair? 3)  #f

procedure: (number? obj)
returns: #t if obj is a number, #f otherwise
procedure: (complex? obj)
returns: #t if obj is a complex number, #f otherwise
procedure: (real? obj)
returns: #t if obj is a real number, #f otherwise
procedure: (rational? obj)
returns: #t if obj is a rational number, #f otherwise
procedure: (integer? obj)
returns: #t if obj is an integer, #f otherwise

These predicates form a hierarchy: any integer is rational, any rational is real, any real is complex, and any complex is numeric. Most implementations do not provide internal representations for irrational numbers, so all real numbers are typically rational as well.

(integer? 1901)  #t
(rational? 1901)  #t
(real? 1901)  #t
(complex? 1901)  #t
(number? 1901)  #t

(integer? -3.0)  #t
(rational? -3.0)  #t
(real? -3.0)  #t
(complex? -3.0)  #t
(number? -3.0)  #t

(integer? 7.0+0.0i)  #t
(rational? 7.0+0.0i)  #t
(real? 7.0+0.0i)  #t
(complex? 7.0+0.0i)  #t
(number? 7.0+0.0i)  #t

(integer? -2/3)  #f
(rational? -2/3)  #t
(real? -2/3)  #t
(complex? -2/3)  #t
(number? -2/3)  #t

(integer? -2.345)  #f
(rational? -2.345)  #t
(real? -2.345)  #t
(complex? -2.345)  #t
(number? -2.345)  #t

(integer? 3.2-2.01i)  #f
(rational? 3.2-2.01i)  #f
(real? 3.2-2.01i)  #f
(complex? 3.2-2.01i)  #t
(number? 3.2-2.01i)  #t

(integer? 'a)  #f
(rational? '(a b c))  #f
(real? "3")  #f
(complex? #(1 2))  #f
(number? #\a)  #f

procedure: (char? obj)
returns: #t if obj is a character, #f otherwise

(char? 'a)  #f
(char? 97)  #f
(char? #\a)  #t
(char? "a")  #f
(char? (string-ref (make-string 1) 0))  #t

procedure: (string? obj)
returns: #t if obj is a string, #f otherwise

(string? "hi")  #t
(string? 'hi)  #f
(string? #\h)  #f

procedure: (vector? obj)
returns: #t if obj is a vector, #f otherwise

(vector? '#())  #t
(vector? '#(a b c))  #t
(vector? (vector 'a 'b 'c))  #t
(vector? '())  #f
(vector? '(a b c))  #f
(vector? "abc")  #f

procedure: (symbol? obj)
returns: #t if obj is a symbol, #f otherwise

(symbol? 't)  #t
(symbol? "t")  #f
(symbol? '(t))  #f
(symbol? #\t)  #f
(symbol? 3)  #f
(symbol? #t)  #f

procedure: (procedure? obj)
returns: #t if obj is a procedure, #f otherwise

(procedure? car)  #t
(procedure? 'car)  #f
(procedure? (lambda (x) x))  #t
(procedure? '(lambda (x) x))  #f
(call/cc procedure?)  #t

Section 6.3. Lists and Pairs

The pair, or cons cell, is the most fundamental of Scheme's structured object types. The most common use for pairs is to build lists, which are ordered sequences of pairs linked one to the next by the cdr field. The elements of the list occupy the car fields of the pairs. The cdr of the last pair in a proper list is the empty list, (); the cdr of the last pair in an improper list can be anything other than ().

Pairs may be used to construct binary trees. Each pair in the tree structure is an internal node of the binary tree; its car and cdr are the children of the node.

Proper lists are printed as sequences of objects separated by whitespace (that is, blanks, tabs, and newlines) and enclosed in parentheses. Brackets ( [ ] ) may also be used in some Scheme systems. For example, (1 2 3) and (a (nested list)) are proper lists. The empty list is written as ().

Improper lists and trees require a slightly more complex syntax. A single pair is written as two objects separated by whitespace and a dot, e.g., (a . b). This is referred to as dotted-pair notation. Improper lists and trees are also written in dotted-pair notation; the dot appears wherever necessary, e.g., (1 2 3 . 4) or ((1 . 2) . 3). Proper lists may be written in dotted-pair notation as well. For example, (1 2 3) may be written as (1 . (2 . (3 . ()))).

Unless otherwise stated, it is an error to pass an improper list to a procedure requiring a list argument.

It is possible to create a circular list or a cyclic graph by destructively altering the car or cdr field of a pair, using set-car! or set-cdr!. Some of the procedures listed in this section may loop indefinitely when handed a cyclic structure.

procedure: (cons obj₁ obj₂)
returns: a new pair whose car and cdr are obj₁ and obj₂

cons is the pair constructor procedure. obj₁ becomes the car and obj₂ becomes the cdr of the new pair.

(cons 'a '())  (a)
(cons 'a '(b c))  (a b c)
(cons 3 4)  (3 . 4)

procedure: (car pair)
returns: the car of pair

It is an error to ask for the car of the empty list.

(car '(a))  a
(car '(a b c))  a
(car (cons 3 4))  3

procedure: (cdr pair)
returns: the cdr of pair

It is an error to ask for the cdr of the empty list.

(cdr '(a))  ()
(cdr '(a b c))  (b c)
(cdr (cons 3 4))  4

procedure: (set-car! pair obj)
returns: unspecified

set-car! changes the car of pair to obj.

(let ((x '(a b c)))
  (set-car! x 1)
  x)  (1 b c)

procedure: (set-cdr! pair obj)
returns: unspecified

set-cdr! changes the cdr of pair to obj.

(let ((x '(a b c)))
  (set-cdr! x 1)
  x)  (a . 1)

procedure: (caar pair)
procedure: (cadr pair)

procedure: (cddddr pair)
returns: the caar, cadr, ..., or cddddr of pair

These procedures are defined as the composition of up to four cars and cdrs. The a's and d's between the c and r represent the application of car or cdr in order from right to left. For example, the procedure cadr applied to a pair yields the car of the cdr of the pair and is equivalent to (lambda (x) (car (cdr x))).

(caar '((a)))  a
(cadr '(a b c))  b
(cdddr '(a b c d))  (d)
(cadadr '(a (b c)))  c

procedure: (list obj ...)
returns: a list of obj ...

list is equivalent to (lambda x x).

(list)  ()
(list 1 2 3)  (1 2 3)
(list 3 2 1)  (3 2 1)

procedure: (list? obj)
returns: #t if obj is a proper list, #f otherwise

list? must return #f for all improper lists, including cyclic lists. A definition of list? is shown on page 64.

(list? '())  #t
(list? '(a b c))  #t
(list? 'a)  #f
(list? '(3 . 4))  #f
(list? 3)  #f
(let ((x (list 'a 'b 'c)))
  (set-cdr! (cddr x) x)
  (list? x))  #f

procedure: (length list)
returns: the number of elements in list

length may be defined as follows.

(define length
  (lambda (ls)
    (let loop ((ls ls) (n 0))
      (if (null? ls)
          n
          (loop (cdr ls) (+ n 1))))))

(length '())  0
(length '(a b c))  3

procedure: (list-ref list n)
returns: the nth element (zero-based) of list

n must be an exact nonnegative integer strictly less than the length of list. list-ref may be defined as follows.

(define list-ref
  (lambda (ls n)
    (if (= n 0)
        (car ls)
        (list-ref (cdr ls) (- n 1)))))

(list-ref '(a b c) 0)  a
(list-ref '(a b c) 1)  b
(list-ref '(a b c) 2)  c

procedure: (list-tail list n)
returns: the nth tail (zero-based) of list

n must be an exact nonnegative integer less than or equal to the length of list. The result is not a copy; the tail is eq? to the nth cdr of list (or to list itself, if n is zero).

list-tail appears in the Revised⁵ Report but not in the ANSI/IEEE standard. It may be defined as follows.

(define list-tail
  (lambda (ls n)
    (if (= n 0)
        ls
        (list-tail (cdr ls) (- n 1)))))

(list-tail '(a b c) 0)  (a b c)
(list-tail '(a b c) 2)  (c)
(list-tail '(a b c) 3)  ()
(list-tail '(a b c . d) 2)  (c . d)
(list-tail '(a b c . d) 3)  d
(let ((x (list 1 2 3)))
  (eq? (list-tail x 2)
       (cddr x)))  #t

procedure: (append list ...)
returns: the concatenation of the input lists

append returns a new list consisting of the elements of the first list followed by the elements of the second list, the elements of the third list, and so on. The new list is made from new pairs for all arguments but the last; the last (which need not actually be a list) is merely placed at the end of the new structure. append may be defined as follows.

(define append
  (lambda args
    (let f ((ls '()) (args args))
      (if (null? args)
          ls
          (let g ((ls ls))
            (if (null? ls)
                (f (car args) (cdr args))
                (cons (car ls) (g (cdr ls)))))))))

(append '(a b c) '())  (a b c)
(append '() '(a b c))  (a b c)
(append '(a b) '(c d))  (a b c d)
(append '(a b) 'c)  (a b . c)
(let ((x (list 'b)))
  (eq? x (cdr (append '(a) x))))  #t

procedure: (reverse list)
returns: a new list containing the elements of list in reverse order

reverse may be defined as follows.

(define reverse
  (lambda (ls)
    (let rev ((ls ls) (new '()))
      (if (null? ls)
          new
          (rev (cdr ls) (cons (car ls) new))))))

(reverse '())  ()
(reverse '(a b c))  (c b a)

procedure: (memq obj list)
procedure: (memv obj list)
procedure: (member obj list)
returns: the first tail of list whose car is equivalent to obj, or #f

These procedures traverse the argument list in order, comparing the elements of list against obj. If an object equivalent to obj is found, the tail of the list whose first element is that object is returned. If the list contains more than one object equivalent to obj, the first tail whose first element is equivalent to obj is returned. If no object equivalent to obj is found, #f is returned. The equivalence test for memq is eq?, for memv is eqv?, and for member is equal?.

These procedures are most often used as predicates, but their names do not end with a question mark because they return a useful true value in place of #t. memq may be defined as follows.

(define memq
  (lambda (x ls)
    (cond
      ((null? ls) #f)
      ((eq? (car ls) x) ls)
      (else (memq x (cdr ls))))))

memv and member may be defined similarly, with eqv? and equal? in place of eq?.

(memq 'a '(b c a d e))  (a d e)
(memq 'a '(b c d e g))  #f
(memq 'a '(b a c a d a))  (a c a d a)

(memv 3.4 '(1.2 2.3 3.4 4.5))  (3.4 4.5)
(memv 3.4 '(1.3 2.5 3.7 4.9))  #f
(let ((ls (list 'a 'b 'c)))
  (set-car! (memv 'b ls) 'z)
  ls)  (a z c)

(member '(b) '((a) (b) (c)))  ((b) (c))
(member '(d) '((a) (b) (c)))  #f
(member "b" '("a" "b" "c"))  ("b" "c")

(define count-occurrences
  (lambda (x ls)
    (cond
      ((memq x ls) =>
       (lambda (ls)
         (+ (count-occurrences x (cdr ls)) 1)))
      (else 0))))

(count-occurrences 'a '(a b c d a))  2

procedure: (assq obj alist)
procedure: (assv obj alist)
procedure: (assoc obj alist)
returns: first element of alist whose car is equivalent to obj, or #f

The argument alist must be an association list. An association list is a proper list whose elements are key-value pairs of the form (key . value). Associations are useful for storing information (values) associated with certain objects (keys).

These procedures traverse the association list, testing each key for equivalence with obj. If an equivalent key is found, the key-value pair is returned. Otherwise, #f is returned.

The equivalence test for assq is eq?, for assv is eqv?, and for assoc is equal?. assq may be defined as follows.

(define assq
  (lambda (x ls)
    (cond
      ((null? ls) #f)
      ((eq? (caar ls) x) (car ls))
      (else (assq x (cdr ls))))))

assv and assoc may be defined similarly, with eqv? and equal? in place of eq?.

(assq 'b '((a . 1) (b . 2)))  (b . 2)
(cdr (assq 'b '((a . 1) (b . 2))))  2
(assq 'c '((a . 1) (b . 2)))  #f

(assv 2/3 '((1/3 . 1) (2/3 . 2)))  (2/3 . 2)
(assv 2/3 '((1/3 . a) (3/4 . b)))  #f

(assoc '(a) '(((a) . a) (-1 . b)))  ((a) . a)
(assoc '(a) '(((b) . b) (a . c)))  #f

(let ((alist '((2 . a) (3 . b))))
  (set-cdr! (assv 3 alist) 'c)
  alist)  ((2 . a) (3 . c))

The interpreter given in Section 9.7 represents environments as association lists and uses assq for both variable lookup and assignment.

Section 6.4. Numbers

Scheme numbers may be classified as integers, rational numbers, real numbers, or complex numbers, although an implementation may support only a subset of these numeric classes. This classification is hierarchical, in that all integers are rational, all rational numbers are real, and all real numbers are complex. The predicates integer?, rational?, real?, and complex? described in Section 6.2 are used to determine into which of these classes a number falls.

A Scheme number may also be classified as exact or inexact, depending upon the quality of operations used to derive the number and the inputs to these operations. The predicates exact? and inexact? may be used to determine the exactness of a number. Most operations on numbers in Scheme are exactness preserving: if given exact operands they return exact values, and if given inexact operands or a combination of exact and inexact operands they return inexact values.

Exact integer and rational arithmetic is typically supported to arbitrary precision; the size of an integer or of the denominator or numerator of a ratio is limited only by system storage constraints. Although other representations are possible, inexact numbers are typically represented by floating-point numbers supported by the host computer's hardware or by system software. Complex numbers are typically represented as ordered pairs (real-part, imag-part), where real-part and imag-part are exact integers, exact rationals, or floating-point numbers.

Scheme numbers are written in a straightforward manner not much different from ordinary conventions for writing numbers. An exact integer is normally written as a sequence of numerals preceded by an optional sign. For example, 3, +19, -100000, and 208423089237489374 all represent exact integers.

An exact rational number is normally written as two sequences of numerals separated by a slash (/) and preceded by an optional sign. For example, 3/4, -6/5, and 1/1208203823 are all exact rational numbers. A ratio is reduced immediately when it is read and may in fact reduce to an exact integer.

Inexact integers and rational numbers are normally written in either floating-point or scientific notation. Floating-point notation consists of a sequence of numerals followed by a decimal point and another sequence of numerals, all preceded by an optional sign. Scientific notation consists of an optional sign, a sequence of numerals, an optional decimal point followed by a second string of numerals, and an exponent; an exponent is written as the letter e followed by an optional sign and a sequence of numerals. For example, 1.0 and -200.0 are valid inexact integers, and 1.5, 0.034, -10e-10 and 1.5e-5 are valid inexact rational numbers. The exponent is the power of ten by which the number preceding the exponent should be scaled, so that 2e3 is equivalent to 2000.0.

The special digit # (hash) may be used in place of a normal digit in certain contexts to signify that the value of the digit is unknown. Numbers that include hash digits are naturally inexact, even if they are written in the style of exact integers or rational numbers. Hash digits may appear after one or more nonhash digits to signify an inexact integer; after one or more nonhash digits in the first or second part of a ratio to specify an inexact rational number; or after one or more nonhash digits before or after the decimal point of an inexact number written in floating-point or scientific notation. No significant (known) digit may follow a hash digit. For example, 1####, -1#/2#, .123### and 1#.### all specify inexact quantities.

Exact and inexact real numbers are written as exact or inexact integers or rational numbers; no provision is made in the syntax of Scheme numbers for nonrational real numbers, i.e., irrational numbers.

Complex numbers may be written in either rectangular or polar form. In rectangular form, a complex number is written as x+yi or x-yi, where x is an integer, rational, or real number and y is an unsigned integer, rational, or real number. The real part, x, may be omitted, in which case it is assumed to be zero. For example, 3+4i, 3.2-3/4i, +i, and -3e-5i are complex numbers written in rectangular form. In polar form, a complex number is written as x@y, where x and y are integer, rational, or real numbers. For example, 1.1@1.764 and -1@-1/2 are complex numbers written in polar form.

The exactness of a numeric representation may be overridden by preceding the representation by either #e or #i. #e forces the number to be exact, and #i forces it to be inexact. For example, 1, #e1, 1/1, #e1/1, #e1.0, #e1e0, and #e1.## all represent the exact integer 1, and #i3/10, 3#/100, 0.3, #i0.3, and 3e-1 all represent the inexact rational 0.3.

Numbers are written by default in base 10, although the special prefixes #b (binary), #o (octal), #d (decimal), and #x (hexadecimal) can be used to specify base 2, base 8, base 10, or base 16. For radix 16, the letters a through f or A through F serve as the additional numerals required to express digit values 10 through 15. For example, #b10101 is the binary equivalent of 21₁₀, #o72 is the octal equivalent of 58₁₀, and #xC7 is the hexadecimal equivalent of 199₁₀. Numbers written in floating-point and scientific notations are always written in base 10.

If both are present, radix and exactness prefixes may appear in either order.

A Scheme implementation may support more than one size of internal representation for inexact quantities. The exponent markers s (short), f (single), d (double), and l (long) may appear in place of the default exponent marker e to override the default size for numbers written in scientific notation. In implementations that support multiple representations, the default size has at least as much precision as double.

A precise grammar for Scheme numbers is included in the description of the formal syntax of Scheme starting on page 277.

Any number can be written in a variety of different ways, but the system printer (see write and display) and number->string express numbers in a compact form, using the fewest number of digits possible while retaining the property that, when read, the printed number is identical to the original number.

The remainder of this section describes procedures that operate on numbers. The type of numeric arguments accepted by these procedures is implied by the name given to the arguments: num for complex numbers (that is, all numbers), real for real numbers, rat for rational numbers, and int for integers.

procedure: (exact? num)
returns: #t if num is exact, #f otherwise

(exact? 1)  #t
(exact? -15/16)  #t
(exact? 2.01)  #f
(exact? #i77)  #f
(exact? #i2/3)  #f
(exact? 1.0-2i)  #f
(exact? -1#i)  #f

procedure: (inexact? num)
returns: #t if num is inexact, #f otherwise

(inexact? -123)  #f
(inexact? #i123)  #t
(inexact? 1e23)  #t
(inexact? 1###)  #t
(inexact? 1#/2#)  #t
(inexact? #e1#/2#)  #f
(inexact? +i)  #f

procedure: (= num₁ num₂ num₃ ...)
procedure: (< real₁ real₂ real₃ ...)
procedure: (> real₁ real₂ real₃ ...)
procedure: (<= real₁ real₂ real₃ ...)
procedure: (>= real₁ real₂ real₃ ...)
returns: #t if the relation holds, #f otherwise

The predicate = returns #t if its arguments are equal. The predicate < returns #t if its arguments are monotonically increasing, i.e., each argument is greater than the preceding ones, while > returns #t if its arguments are monotonically decreasing. The predicate <= returns #t if its arguments are monotonically nondecreasing, i.e., each argument is not less than the preceding ones, while >= returns #t if its arguments are monotonically nonincreasing.

As implied by the names of the arguments, = is defined for complex arguments while the other relational predicates are defined only for real arguments. Two complex numbers are considered equal if their real and imaginary parts are equal.

(= 7 7)  #t
(= 7 9)  #f

(< 2e3 3e2)  #f
(<= 1 2 3 3 4 5)  #t
(<= 1 2 3 4 5)  #t

(> 1 2 2 3 3 4)  #f
(>= 1 2 2 3 3 4)  #f

(= -1/2 -0.5)  #t
(= 2/3 .667)  #f
(= 7.2+0i 7.2)  #t
(= 7.2-3i 7)  #f

(< 1/2 2/3 3/4)  #t
(> 8 4.102 2/3 -5)  #t

(let ((x 0.218723452))
  (< 0.210 x 0.220))  #t

(let ((i 1) (v (vector 'a 'b 'c)))
  (< -1 i (vector-length v)))  #t

(apply < '(1 2 3 4))  #t
(apply > '(4 3 3 2))  #f

procedure: (+ num ...)
returns: the sum of the arguments num ...

When called with no arguments, + returns 0.

(+)  0
(+ 1 2)  3
(+ 1/2 2/3)  7/6
(+ 3 4 5)  12
(+ 3.0 4)  7.0
(+ 3+4i 4+3i)  7+7i
(apply + '(1 2 3 4 5))  15

procedure: (- num₁)
procedure: (- num₁ num₂ num₃ ...)
returns: see explanation

When called with one argument, - returns the negative of num₁. Thus, (- num₁) is an idiom for (- 0 num₁).

When called with two or more arguments, - returns the result of subtracting the sum of the numbers num₂ ... from num₁.

The ANSI/IEEE standard includes only one- and two-argument variants. The more general form is included in the Revised⁵ Report.

(- 3)  -3
(- -2/3)  2/3
(- 4 3.0)  1.0
(- 3.25+4.25i 1/4+1/4i)  3.0+4.0i
(- 4 3 2 1)  -2

procedure: (* num ...)
returns: the product of the arguments num ...

When called with no arguments, * returns 1.

(*)  1
(* 3.4)  3.4
(* 1 1/2)  1/2
(* 3 4 5.5)  66.0
(* 1+2i 3+4i)  -5+10i
(apply * '(1 2 3 4 5))  120

procedure: (/ num₁)
procedure: (/ num₁ num₂ num₃ ...)
returns: see explanation

When called with one argument, / returns the reciprocal of num₁. That is, (/ num₁) is an idiom for (/ 1 num₁).

When called with two or more arguments, / returns the result of dividing num₁ by the product of the remaining arguments num₂ ....

The ANSI/IEEE standard includes only one- and two-argument variants. The more general form is included in the Revised⁵ Report.

(/ -17)  -1/17
(/ 1/2)  2
(/ .5)  2.0
(/ 3 4)  3/4
(/ 3.0 4)  .75
(/ -5+10i 3+4i)  1+2i
(/ 60 5 4 3 2)  1/2

procedure: (zero? num)
returns: #t if num is zero, #f otherwise

zero? is equivalent to (lambda (x) (= x 0)).

(zero? 0)  #t
(zero? 1)  #f
(zero? (- 3.0 3.0))  #t
(zero? (+ 1/2 1/2))  #f
(zero? 0+0i)  #t
(zero? 0.0-0.0i)  #t

procedure: (positive? real)
returns: #t if real is greater than zero, #f otherwise

positive? is equivalent to (lambda (x) (> x 0)).

(positive? 128)  #t
(positive? 0.0)  #f
(positive? 1.8e-15)  #t
(positive? -2/3)  #f
(positive? .001-0.0i)  #t

procedure: (negative? real)
returns: #t if real is less than zero, #f otherwise

negative? is equivalent to (lambda (x) (< x 0)).

(negative? -65)  #t
(negative? 0)  #f
(negative? -0.0121)  #t
(negative? 15/16)  #f
(negative? -7.0+0.0i)  #t

procedure: (even? int)
returns: #t if int is even, #f otherwise

(even? 0)  #t
(even? 1)  #f
(even? 2.0)  #t
(even? -120762398465)  #f
(even? 2.0+0.0i)  #t

procedure: (odd? int)
returns: #t if int is odd, #f otherwise

(odd? 0)  #f
(odd? 1)  #t
(odd? 2.0)  #f
(odd? -120762398465)  #t
(odd? 2.0+0.0i)  #f

procedure: (quotient int₁ int₂)
returns: the integer quotient of int₁ and int₂

(quotient 45 6)  7
(quotient 6.0 2.0)  3.0
(quotient 3.0 -2)  -1.0

procedure: (remainder int₁ int₂)
returns: the integer remainder of int₁ and int₂

The result of remainder has the same sign as int₁.

(remainder 16 4)  0
(remainder 5 2)  1
(remainder -45.0 7)  -3.0
(remainder 10.0 -3.0)  1.0
(remainder -17 -9)  -8

procedure: (modulo int₁ int₂)
returns: the integer modulus of int₁ and int₂

The result of modulo has the same sign as int₂.

(modulo 16 4)  0
(modulo 5 2)  1
(modulo -45.0 7)  4.0
(modulo 10.0 -3.0)  -2.0
(modulo -17 -9)  -8

procedure: (truncate real)
returns: the integer closest to real toward zero

(truncate 19)  19
(truncate 2/3)  0
(truncate -2/3)  0
(truncate 17.3)  17.0
(truncate -17/2)  -8

procedure: (floor real)
returns: the integer closest to real toward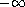

(floor 19)  19
(floor 2/3)  0
(floor -2/3)  -1
(floor 17.3)  17.0
(floor -17/2)  -9

procedure: (ceiling real)
returns: the integer closest to real toward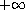

(ceiling 19)  19
(ceiling 2/3)  1
(ceiling -2/3)  0
(ceiling 17.3)  18.0
(ceiling -17/2)  -8

procedure: (round real)
returns: the integer closest to real

If real is exactly between two integers, the closest even integer is returned.

(round 19)  19
(round 2/3)  1
(round -2/3)  -1
(round 17.3)  17.0
(round -17/2)  -8
(round 2.5)  2.0
(round 3.5)  4.0

procedure: (abs real)
returns: the absolute value of real

abs is equivalent to (lambda (x) (if (< x 0) (- x) x)). abs and magnitude (see page 150) are identical for real inputs.

(abs 1)  1
(abs -3/4)  3/4
(abs 1.83)  1.83
(abs -0.093)  0.093

procedure: (max real₁ real₂ ...)
returns: the maximum of real₁ real₂ ...

(max 4 -7 2 0 -6)  4
(max 1/2 3/4 4/5 5/6 6/7)  6/7
(max 1.5 1.3 -0.3 0.4 2.0 1.8)  2.0
(max 5 2.0)  5.0
(max -5 -2.0)  -2.0
(let ((ls '(7 3 5 2 9 8)))
  (apply max ls))  9

procedure: (min real₁ real₂ ...)
returns: the minimum of real₁ real₂ ...

(min 4 -7 2 0 -6)  -7
(min 1/2 3/4 4/5 5/6 6/7)  1/2
(min 1.5 1.3 -0.3 0.4 2.0 1.8)  -0.3
(min 5 2.0)  2.0
(min -5 -2.0)  -5.0
(let ((ls '(7 3 5 2 9 8)))
  (apply min ls))  2

procedure: (gcd int ...)
returns: the greatest common divisor of its arguments int ...

The result is always nonnegative, i.e., factors of -1 are ignored. When called with no arguments, gcd returns 0.

(gcd)  0
(gcd 34)  34
(gcd 33.0 15.0)  3.0
(gcd 70 -42 28)  14

procedure: (lcm int ...)
returns: the least common multiple of its arguments int ...

The result is always nonnegative, i.e., common multiples of -1 are ignored. Although lcm should probably return when called with no arguments, it is defined to return 1. If one or more of the arguments is 0, lcm returns 0.

(lcm)  1
(lcm 34)  34
(lcm 33.0 15.0)  165.0
(lcm 70 -42 28)  420
(lcm 17.0 0)  0

procedure: (expt num₁ num₂)
returns: num₁ raised to the num₂ power

If both arguments are 0, expt returns 1.

(expt 2 10)  1024
(expt 2 -10)  1/1024
(expt 2 -10.0)  9.765625e-4
(expt -1/2 5)  -1/32
(expt 3.0 3)  27.0
(expt +i 2)  -1

procedure: (exact->inexact num)
returns: an inexact representation for num

If num is already inexact, it is returned unchanged. If no inexact representation for num is supported by the implementation, an error may be signaled.

(exact->inexact 3)  3.0
(exact->inexact 3.0)  3.0
(exact->inexact -1/4)  -.25
(exact->inexact 3+4i)  3.0+4.0i
(exact->inexact (expt 10 20))  1e20

procedure: (inexact->exact num)
returns: an exact representation for num

If num is already exact, it is returned unchanged. If no exact representation for num is supported by the implementation, an error may be signaled.

(inexact->exact 3.0)  3
(inexact->exact 3)  3
(inexact->exact -.25)  -1/4
(inexact->exact 3.0+4.0i)  3+4i
(inexact->exact 1e20)  100000000000000000000

procedure: (rationalize real₁ real₂)
returns: see below

rationalize returns the simplest rational number that differs from real₁ by no more than real₂. A rational number q₁ = n₁/m₁ is simpler than another rational number q₂ = n₂/m₂ if |n₁| ≤ |n₂| and |m₁| ≤ |m₂| and either |n₁| < |n₂| or |m₁| < |m₂|.

(rationalize 3/10 1/10)  1/3
(rationalize .3 1/10)  0.3333333333333333
(eqv? (rationalize .3 1/10) #i1/3)  #t

procedure: (numerator rat)
returns: the numerator of rat

If rat is an integer, the numerator is rat.

(numerator 9)  9
(numerator 9.0)  9.0
(numerator 2/3)  2
(numerator -9/4)  -9
(numerator -2.25)  -9.0

procedure: (denominator rat)
returns: the denominator of rat

If rat is an integer, the denominator is 1.

(denominator 9)  1
(denominator 9.0)  1.0
(denominator 2/3)  3
(denominator -9/4)  4
(denominator -2.25)  4.0

procedure: (real-part num)
returns: the real component of num

If num is real, real-part returns num.

(real-part 3+4i)  3
(real-part -2.3+0.7i)  -2.3
(real-part -i)  0
(real-part 17.2)  17.2
(real-part -17/100)  -17/100

procedure: (imag-part num)
returns: the imaginary component of num

If num is real, imag-part returns zero.

(imag-part 3+4i)  4
(imag-part -2.3+0.7i)  0.7
(imag-part -i)  -1
(imag-part 17.2)  0.0
(imag-part -17/100)  0

procedure: (make-rectangular real₁ real₂)
returns: a complex number with real component real₁ and imaginary component real₂

(make-rectangular -2 7)  -2+7i
(make-rectangular 2/3 -1/2)  2/3-1/2i
(make-rectangular 3.2 5.3)  3.2+5.3i

procedure: (make-polar real₁ real₂)
returns: a complex number with magnitude real₁ and angle real₂

(make-polar 2 0)  2
(make-polar 2.0 0.0)  2.0+0.0i
(make-polar 1.0 (asin -1.0))  0.0-1.0i
(eqv? (make-polar 7.2 -0.588) 7.2@-0.588)  #t

procedure: (angle num)
returns: the angle part of the polar representation of num

The range of the result is 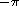(exclusive) to 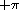(inclusive).

(angle 7.3@1.5708)  1.5708
(angle 5.2)  0.0

procedure: (magnitude num)
returns: the magnitude of num

magnitude and abs (see page 146) are identical for real arguments. The magnitude of a complex number x + yi is .

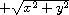(magnitude 1)  1
(magnitude -3/4)  3/4
(magnitude 1.83)  1.83
(magnitude -0.093)  0.093
(magnitude 3+4i)  5
(magnitude 7.25@1.5708)  7.25

procedure: (sqrt num)
returns: the principal square root of num

Implementations are encouraged, but not required, to return exact results for exact inputs to sqrt whenever feasible.

(sqrt 16)  4
(sqrt 1/4)  1/2
(sqrt 4.84)  2.2
(sqrt -4.84)  0.0+2.2i
(sqrt 3+4i)  2+1i
(sqrt -3.0-4.0i)  1.0-2.0i

procedure: (exp num)
returns: e to the num power

(exp 0.0)  1.0
(exp 1.0)  2.7182818284590455
(exp -.5)  0.6065306597126334

procedure: (log num)
returns: the natural log of num

The log of a complex number z is defined as follows.

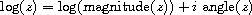
(log 1.0)  0.0
(log (exp 1.0))  1.0
(/ (log 100) (log 10))  2.0
(log (make-polar (exp 2.0) 1.0))  2.0+1.0i

procedure: (sin num)
procedure: (cos num)
procedure: (tan num)
returns: the sine, cosine, or tangent of num

The argument is specified in radians.

procedure: (asin num)
procedure: (acos num)
returns: the arc sine or the arc cosine of num

The result is in radians. The arc sine and arc cosine of a complex number z are defined as follows.

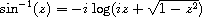
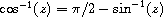
procedure: (atan num)
procedure: (atan real₁ real₂)
returns: see explanation

When passed a single complex argument num (the first form), atan returns the arc tangent of num. The arc tangent of a complex number z is defined as follows.

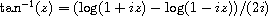
When passed two real arguments (the second form), atan is equivalent to (lambda (y x) (angle (make-rectangular x y))).

procedure: (string->number string)
procedure: (string->number string radix)
returns: the number represented by string, or #f

If string is a valid representation of a number, that number is returned, otherwise #f is returned. The number is interpreted in radix radix, which must be an exact integer in the set {2,8,10,16}. If not specified, radix defaults to 10. Any radix specifier within string, e.g., #x, overrides the radix argument.

(string->number "0")  0
(string->number "3.4e3")  3400.0
(string->number "#x#e-2e2")  -738
(string->number "#e-2e2" 16)  -738
(string->number "#i15/16")  0.9375
(string->number "10" 16)  16

procedure: (number->string num)
procedure: (number->string num radix)
returns: an external representation of num as a string

The num is expressed in radix radix, which must be an exact integer in the set {2,8,10,16}. If not specified, radix defaults to 10. In any case, no radix specifier appears in the resulting string.

The external representation is such that, when converted back into a number using string->number, the resulting numeric value is equivalent to num. That is, for all inputs:

(eqv? (string->number
        (number->string num radix)
        radix)
      num)

returns #t. Inexact results are expressed using the fewest number of significant digits possible without violating the above restriction.

(number->string 3.4)  "3.4"
(number->string 1e2)  "100.0"
(number->string 1e23)  "1e23"
(number->string -7/2)  "-7/2"
(number->string 220/9 16)  "DC/9"

Section 6.5. Characters

Characters are atomic objects representing letters, digits, special symbols such as $ or -, and certain nongraphic control characters such as space and newline. Characters are written with a #\ prefix. For most characters, the prefix is followed by the character itself. The written character representation of the letter A, for example, is #\A. The characters newline and space may be written in this manner as well, but they can also be written as #\newline or #\space.

This section describes the operations that deal primarily with characters. See also the following section on strings and Chapter 7 on input and output for other operations relating to characters.

procedure: (char=? char₁ char₂ char₃ ...)
procedure: (char<? char₁ char₂ char₃ ...)
procedure: (char>? char₁ char₂ char₃ ...)
procedure: (char<=? char₁ char₂ char₃ ...)
procedure: (char>=? char₁ char₂ char₃ ...)
returns: #t if the relation holds, #f otherwise

These predicates behave in a similar manner to the numeric predicates =, <, >, <=, and >=. For example, char=? returns #t when its arguments are equivalent characters, and char<? returns #t when its arguments are monotonically increasing character values.

Independent of the particular representation employed, the following relationships are guaranteed to hold.

• The lower-case letters #\a through #\z are in order from low to high; e.g., #\d is less than #\e.

• The upper-case letters #\A through #\Z are in order from low to high; e.g., #\Q is less than #\R.

• The digits #\0 through #\9 are in order from low to high; e.g., #\3 is less than #\4.

• All digits precede all lower-case letters, or all lower-case letters precede all digits.

• All digits precede all upper-case letters, or all upper-case letters precede all digits.

The tests performed by char=?, char<?, char>?, char<=?, and char>=? are case-sensitive. That is, the character #\A is not equivalent to the character #\a according to these predicates.

The ANSI/IEEE standard includes only two-argument versions of these procedures. The more general versions are mentioned in the Revised⁵ Report.

(char>? #\a #\b)  #f
(char<? #\a #\b)  #t
(char<? #\a #\b #\c)  #t
(let ((c #\r))
  (char<=? #\a c #\z))  #t
(char<=? #\Z #\W)  #f
(char=? #\+ #\+)  #t
(or (char<? #\a #\0)
    (char<? #\0 #\a))  #t

procedure: (char-ci=? char₁ char₂ char₃ ...)
procedure: (char-ci<? char₁ char₂ char₃ ...)
procedure: (char-ci>? char₁ char₂ char₃ ...)
procedure: (char-ci<=? char₁ char₂ char₃ ...)
procedure: (char-ci>=? char₁ char₂ char₃ ...)
returns: #t if the relation holds, #f otherwise

These predicates are identical to the predicates char=?, char<?, char>?, char<=?, and char>=? except that they are case-insensitive. This means that when two letters are compared, case is unimportant. For example, char=? considers #\a and #\A to be distinct values; char-ci=? does not.

The ANSI/IEEE standard includes only two-argument versions of these procedures. The more general versions are mentioned in the Revised⁵ Report.

(char-ci<? #\a #\B)  #t
(char-ci=? #\W #\w)  #t
(char-ci=? #\= #\+)  #f
(let ((c #\R))
  (list (char<=? #\a c #\z)
        (char-ci<=? #\a c #\z)))  (#f #t)

procedure: (char-alphabetic? char)
returns: #t if char is a letter, #f otherwise

(char-alphabetic? #\a)  #t
(char-alphabetic? #\T)  #t
(char-alphabetic? #\8)  #f
(char-alphabetic? #\$)  #f

procedure: (char-numeric? char)
returns: #t if char is a digit, #f otherwise

(char-numeric? #\7)  #t
(char-numeric? #\2)  #t
(char-numeric? #\X)  #f
(char-numeric? #\space)  #f

procedure: (char-lower-case? letter)
returns: #t if letter is lower-case, #f otherwise

If letter is not alphabetic, the result is unspecified.

(char-lower-case? #\r)  #t
(char-lower-case? #\R)  #f
(char-lower-case? #\8)  unspecified

procedure: (char-upper-case? letter)
returns: #t if letter is upper-case, #f otherwise

If letter is not alphabetic, the result is unspecified.

(char-upper-case? #\r)  #f
(char-upper-case? #\R)  #t
(char-upper-case? #\8)  unspecified

procedure: (char-whitespace? char)
returns: #t if char is whitespace, #f otherwise

Whitespace consists of spaces and newlines and possibly other nongraphic characters, depending upon the Scheme implementation and the underlying operating system.

(char-whitespace? #\space)  #t
(char-whitespace? #\newline)  #t
(char-whitespace? #\Z)  #f

procedure: (char-upcase char)
returns: the upper-case character equivalent to char

If char is a lower-case character, char-upcase returns the upper-case equivalent. If char is not a lower-case character, char-upcase returns char.

(char-upcase #\g)  #\G
(char-upcase #\Y)  #\Y
(char-upcase #\7)  #\7

procedure: (char-downcase char)
returns: the lower-case character equivalent to char

If char is an upper-case character, char-downcase returns the lower-case equivalent. If char is not an upper-case character, char-downcase returns char.

(char-downcase #\g)  #\g
(char-downcase #\Y)  #\y
(char-downcase #\7)  #\7

procedure: (char->integer char)
returns: an exact integer representation for char

char->integer is useful for performing table lookups, with the integer representation of char employed as an index into a table. The integer representation of a character is typically the integer code supported by the operating system for character input and output.

Although the particular representation employed depends on the Scheme implementation and the underlying operating system, the rules regarding the relationship between character objects stated above under the description of char=? and its relatives holds for the integer representations of characters as well.

The following examples assume that the integer representation is the ASCII code for the character.

(char->integer #\h)  104
(char->integer #\newline)  10

The definition of make-dispatch-table below shows how the integer codes returned by char->integer may be used portably to associate values with characters in vector-based dispatch tables, even though the exact correspondence between characters and their integer codes is unspecified.

make-dispatch-table accepts two arguments: an association list (see assv in Section 6.3) associating characters with values and a default value for characters without associations. It returns a lookup procedure that accepts a character and returns the associated (or default) value. make-dispatch-table builds a vector that is used by the lookup procedure. This vector is indexed by the integer codes for the characters and contains the associated values. Slots in the vector between indices for characters with defined values are filled with the default value. The code works even if char->integer returns negative values or both negative and nonnegative values, although the table can get large if the character codes are not tightly packed.

(define make-dispatch-table
  (lambda (alist default)
    (let ((codes (map char->integer (map car alist))))
      (let ((first-index (apply min codes))
            (last-index (apply max codes)))
        (let ((n (+ (- last-index first-index) 1)))
          (let ((v (make-vector n default)))
            (for-each
              (lambda (i x) (vector-set! v (- i first-index) x))
              codes
              (map cdr alist))
            ;; table is built; return the table lookup procedure
            (lambda (c)
              (let ((i (char->integer c)))
                (if (<= first-index i last-index)
                    (vector-ref v (- i first-index))
                    default)))))))))

(define-syntax define-dispatch-table
  ;; define-dispatch-table associates sets of characters in strings
  ;; with values in a call to make-dispatch-table.
  (syntax-rules ()
    ((_ default (str val) ...)
     (make-dispatch-table
       (append (map (lambda (c) (cons c 'val))
                    (string->list str))
               ...)
       'default))))

(define t
  (define-dispatch-table
    unknown
    ("abcdefghijklmnopqrstuvwxyz" letter)
    ("ABCDEFGHIJKLMNOPQRSTUVWXYZ" letter)
    ("0123456789" digit)))

(t #\m)  letter
(t #\0)  digit
(t #\*)  unknown

procedure: (integer->char int)
returns: the character object corresponding to the exact integer int

This procedure is the functional inverse of char->integer. It is an error for int to be outside the range of valid integer character codes.

The following examples assume that the integer representation is the ASCII code for the character.

(integer->char 48)  #\0
(integer->char 101)  #\e

Section 6.6. Strings

Strings are sequences of characters and are typically used as messages or character buffers. Scheme provides operations for creating strings, extracting characters from strings, obtaining substrings, concatenating strings, and altering the contents of strings.

A string is written as a sequence of characters enclosed in double quotes, e.g., "hi there". A double quote may be introduced into a string by preceding it by a backward slash, e.g., "two \"quotes\" within". A backward slash may also be included by preceding it with a backward slash, e.g., "a \\slash".

Strings are indexed by exact nonnegative integers, and the index of the first element of any string is 0. The highest valid index for a given string is one less than its length.

procedure: (string=? string₁ string₂ string₃ ...)
procedure: (string<? string₁ string₂ string₃ ...)
procedure: (string>? string₁ string₂ string₃ ...)
procedure: (string<=? string₁ string₂ string₃ ...)
procedure: (string>=? string₁ string₂ string₃ ...)
returns: #t if the relation holds, #f otherwise

As with =, <, >, <=, and >=, these predicates express relationships among all of the arguments. For example, string>? determines if the lexicographic ordering of its arguments is monotonically decreasing.

The comparisons are based on the character predicates char=?, char<?, char>?, char<=?, and char>=?. Two strings are lexicographically equivalent if they are the same length and consist of the same sequence of characters according to char=?. If two strings differ only in length, the shorter string is considered to be lexicographically less than the longer string. Otherwise, the first character position at which the strings differ determines which string is lexicographically less than the other, according to char<?.

The ANSI/IEEE standard includes only two-argument versions of these procedures. The more general versions are mentioned in the Revised⁵ Report.

Two-argument string=? may be defined as follows.

(define string=?
  (lambda (s1 s2)
    (let ((n (string-length s1)))
      (and (= (string-length s2) n)
           (let loop ((i 0))
             (or (= i n)
                 (and (char=? (string-ref s1 i) (string-ref s2 i))
                      (loop (+ i 1)))))))))

Two-argument string<? may be defined as follows.

(define string<?
  (lambda (s1 s2)
    (let ((n1 (string-length s1)) (n2 (string-length s2)))
      (let loop ((i 0))
        (and (not (= i n2))
             (or (= i n1)
                 (let ((c1 (string-ref s1 i)) (c2 (string-ref s2 i)))
                   (or (char<? c1 c2)
                       (and (char=? c1 c2)
                            (loop (+ i 1)))))))))))

These definitions may be extended straightforwardly to support three or more arguments. string<=?, string>?, and string>=? may be defined similarly.

(string=? "mom" "mom")  #t
(string<? "mom" "mommy")  #t
(string>? "Dad" "Dad")  #f
(string=? "Mom and Dad" "mom and dad")  #f
(string<? "a" "b" "c")  #t

procedure: (string-ci=? string₁ string₂ string₃ ...)
procedure: (string-ci<? string₁ string₂ string₃ ...)
procedure: (string-ci>? string₁ string₂ string₃ ...)
procedure: (string-ci<=? string₁ string₂ string₃ ...)
procedure: (string-ci>=? string₁ string₂ string₃ ...)
returns: #t if the relation holds, #f otherwise

These predicates are case-insensitive versions of string=?, string<?, string>?, string<=?, and string>=?. That is, the comparisons are based on the character predicates char-ci=?, char-ci<?, char-ci>?, char-ci<=?, and char-ci>=?.

The ANSI/IEEE standard includes only two-argument versions of these procedures. The more general versions are mentioned in the Revised⁵ Report.

Two-argument versions of these procedures may be defined in a manner similar to string=? and string<? above.

(string-ci=? "Mom and Dad" "mom and dad")  #t
(string-ci<=? "say what" "Say What!?")  #t
(string-ci>? "N" "m" "L" "k")  #t

procedure: (string char ...)
returns: a string containing the characters char ...

(string)  ""
(string #\a #\b #\c)  "abc"
(string #\H #\E #\Y #\!)  "HEY!"

procedure: (make-string n)
procedure: (make-string n char)
returns: a string of length n

n must be an exact nonnegative integer. If char is supplied, the string is filled with char, otherwise the characters contained in the string are unspecified.

(make-string 0)  ""
(make-string 0 #\x)  ""
(make-string 5 #\x)  "xxxxx"

procedure: (string-length string)
returns: the number of characters in string

The length of a string is always an exact nonnegative integer.

(string-length "abc")  3
(string-length "")  0
(string-length "hi there")  8
(string-length (make-string 1000000))  1000000

procedure: (string-ref string n)
returns: the nth character (zero-based) of string

n must be an exact nonnegative integer strictly less than the length of string.

(string-ref "hi there" 0)  #\h
(string-ref "hi there" 5)  #\e

procedure: (string-set! string n char)
returns: unspecified

n must be an exact nonnegative integer strictly less than the length of string. string-set! changes the nth element of string to char.

(let ((str "hi three"))
  (string-set! str 5 #\e)
  (string-set! str 6 #\r)
  str)  "hi there"

procedure: (string-copy string)
returns: a new copy of string

string-copy is equivalent to (lambda (s) (string-append s)). string-copy appears in the Revised⁵ Report but not in the ANSI/IEEE standard.

(string-copy "abc")  "abc"
(let ((str "abc"))
  (eq? str (string-copy str)))  #f

procedure: (string-append string ...)
returns: a new string formed by concatenating the strings string ...

(string-append)  ""
(string-append "abc" "def")  "abcdef"
(string-append "Hey " "you " "there!")  "Hey you there!"

The following implementation of string-append recurs down the list of strings to compute the total length, then allocates the new string and fills it up as it unwinds the recursion.

(define string-append
  (lambda args
    (let f ((ls args) (n 0))
      (if (null? ls)
          (make-string n)
          (let* ((s1 (car ls))
                 (m (string-length s1))
                 (s2 (f (cdr ls) (+ n m))))
            (do ((i 0 (+ i 1)) (j n (+ j 1)))
                ((= i m) s2)
                (string-set! s2 j (string-ref s1 i))))))))

procedure: (substring string start end)
returns: a copy of string from start (inclusive) to end (exclusive)

start and end must be exact nonnegative integers; start must be strictly less than the length of string, while end may be less than or equal to the length of string. If end ≤ start, a string of length zero is returned. substring may be defined as follows.

(define substring
  (lambda (s1 m n)
    (let ((s2 (make-string (- n m))))
      (do ((j 0 (+ j 1)) (i m (+ i 1)))
          ((= i n) s2)
          (string-set! s2 j (string-ref s1 i))))))

(substring "hi there" 0 1)  "h"
(substring "hi there" 3 6)  "the"
(substring "hi there" 5 5)  ""

(let ((str "hi there"))
  (let ((end (string-length str)))
    (substring str 0 end)))  "hi there"

procedure: (string-fill! string char)
returns: unspecified

string-fill! sets every character in string to char. string-fill! appears in the Revised⁵ Report but not in the ANSI/IEEE standard. It may be defined as follows.

(define string-fill!
  (lambda (s c)
    (let ((n (string-length s)))
      (do ((i 0 (+ i 1)))
          ((= i n))
          (string-set! s i c)))))

(let ((str (string-copy "sleepy")))
  (string-fill! str #\Z)
  str)  "ZZZZZZ"

procedure: (string->list string)
returns: a list of the characters in string

string->list allows a string to be converted into a list, so that Scheme's list-processing operations may be applied to the processing of strings. string->list appears in the Revised⁵ Report but not in the ANSI/IEEE standard. It may be defined as follows.

(define string->list
  (lambda (s)
    (do ((i (- (string-length s) 1) (- i 1))
         (ls '() (cons (string-ref s i) ls)))
        ((< i 0) ls))))

(string->list "")  ()
(string->list "abc")  (#\a #\b #\c)
(apply char<? (string->list "abc"))  #t
(map char-upcase (string->list "abc"))  (#\A #\B #\C)

procedure: (list->string list)
returns: a string of the characters in list

list must consist entirely of characters.

list->string is the functional inverse of string->list. A program might use both procedures together, first converting a string into a list, then operating on this list to produce a new list, and finally converting the new list back into a string.

list->string appears in the Revised⁵ Report but not in the ANSI/IEEE standard. It may be defined as follows.

(define list->string
  (lambda (ls)
    (let ((s (make-string (length ls))))
      (do ((ls ls (cdr ls)) (i 0 (+ i 1)))
          ((null? ls) s)
          (string-set! s i (car ls))))))

(list->string '())  ""
(list->string '(#\a #\b #\c))  "abc"
(list->string
  (map char-upcase
       (string->list "abc")))  "ABC"

Section 6.7. Vectors

Vectors are more convenient and efficient than lists for some applications. Whereas accessing an arbitrary element in a list requires a linear traversal of the list up to the selected element, arbitrary vector elements are accessed in constant time. The length of a vector in Scheme is the number of elements it contains. Vectors are indexed by exact nonnegative integers, and the index of the first element of any vector is 0. The highest valid index for a given vector is one less than its length.

As with lists, the elements of a vector may be of any type; a single vector may even hold more than one type of object.

A vector is written as a sequence of objects separated by whitespace, preceded by the prefix #( and followed by ). For example, a vector consisting of the elements a, b, and c would be written #(a b c).

procedure: (vector obj ...)
returns: a vector of the objects obj ...

(vector)  #()
(vector 'a 'b 'c)  #(a b c)

procedure: (make-vector n)
procedure: (make-vector n obj)
returns: a vector of length n

n must be an exact nonnegative integer. If obj is supplied, each element of the vector is filled with obj; otherwise, the elements are unspecified.

(make-vector 0)  #()
(make-vector 0 'a)  #()
(make-vector 5 'a)  #(a a a a a)

procedure: (vector-length vector)
returns: the number of elements in vector

The length of a vector is always an exact nonnegative integer.

(vector-length '#())  0
(vector-length '#(a b c))  3
(vector-length (vector 1 2 3 4))  4
(vector-length (make-vector 300))  300

procedure: (vector-ref vector n)
returns: the nth element (zero-based) of vector

n must be an exact nonnegative integer strictly less than the length of vector.

(vector-ref '#(a b c) 0)  a
(vector-ref '#(a b c) 1)  b
(vector-ref '#(x y z w) 3)  w

procedure: (vector-set! vector n obj)
returns: unspecified

n must be an exact nonnegative integer strictly less than the length of vector. vector-set! changes the nth element of vector to obj.

(let ((v (vector 'a 'b 'c 'd 'e)))
  (vector-set! v 2 'x)
  v)  #(a b x d e)

procedure: (vector-fill! vector obj)
returns: unspecified

vector-fill! replaces each element of vector with obj. vector-fill! appears in the Revised⁵ Report but not in the ANSI/IEEE standard. It may be defined as follows.

(define vector-fill!
  (lambda (v x)
    (let ((n (vector-length v)))
      (do ((i 0 (+ i 1)))
          ((= i n))
          (vector-set! v i x)))))

(let ((v (vector 1 2 3)))
  (vector-fill! v 0)
  v)  #(0 0 0)

procedure: (vector->list vector)
returns: a list of the elements of vector

vector->list provides a convenient method for applying list-processing operations to vectors. vector->list appears in the Revised⁵ Report but not in the ANSI/IEEE standard. It may be defined as follows.

(define vector->list
  (lambda (s)
    (do ((i (- (vector-length s) 1) (- i 1))
         (ls '() (cons (vector-ref s i) ls)))
        ((< i 0) ls))))

(vector->list (vector))  ()
(vector->list '#(a b c))  (a b c)

(let ((v '#(1 2 3 4 5)))
  (apply * (vector->list v)))  120

procedure: (list->vector list)
returns: a vector of the elements of list

list->vector is the functional inverse of vector->list. The two procedures are often used in combination to take advantage of a list-processing operation. A vector may be converted to a list with vector->list, this list processed in some manner to produce a new list, and the new list converted back into a vector with list->vector.

list->vector appears in the Revised⁵ Report but not in the ANSI/IEEE standard. It may be defined as follows.

(define list->vector
  (lambda (ls)
    (let ((s (make-vector (length ls))))
      (do ((ls ls (cdr ls)) (i 0 (+ i 1)))
          ((null? ls) s)
          (vector-set! s i (car ls))))))

(list->vector '())  #()
(list->vector '(a b c))  #(a b c)

(let ((v '#(1 2 3 4 5)))
  (let ((ls (vector->list v)))
    (list->vector (map * ls ls))))  #(1 4 9 16 25)

Section 6.8. Symbols

Symbols are used for a variety of purposes as symbolic names in Scheme programs. Strings could be used for most of the same purposes, but an important characteristic of symbols makes comparisons between symbols much more efficient. This characteristic is that two symbols with the same name are identical in the sense of eq?. The reason is that the Scheme reader (see read in Section 7.1) and the procedure string->symbol catalog symbols in an internal symbol table and always return the same symbol whenever the same name is encountered. Thus, no character-by-character comparison is needed, as would be needed to compare two strings.

The property that two symbols may be compared quickly for equivalence makes them ideally suited for use as identifiers in the representation of programs, allowing fast comparison of identifiers. This property also makes symbols useful for a variety of other purposes. For example, symbols might be used as messages passed between procedures, labels for list-structured records, or names for objects stored in an association list (see assq in Section 6.3).

Symbols are written without double quotes or other bracketing characters. Parentheses, double quotes, spaces, and most other characters with a special meaning to the Scheme reader are not allowed within the printed representation of a symbol. Some implementations, however, support the use of backward slashes to escape special characters occurring in symbols, in a manner similar to the use of backward slashes in strings.

Refer to Section 1.1 or the formal syntax of Scheme at the back of this book for a precise description of the syntax of symbols.

procedure: (string->symbol string)
returns: a symbol whose name is string

string->symbol records all symbols it creates in an internal table that it shares with the system reader, read. If a symbol whose name is equivalent to string (according to the predicate string=?) already exists in the table, this symbol is returned. Otherwise, a new symbol is created with string as its name; this symbol is entered into the table and returned.

The system reader arranges to convert all symbols to a single case (lower case is assumed in this book), before entering them into the internal table. string->symbol does not. Thus, it is possible to produce symbols in lower case, upper case, or even mixed case, using string->symbol. It is also possible to create symbols with names that contain special characters, such as spaces or parentheses.

(string->symbol "x")  x

(eq? (string->symbol "x") 'x)  #t
(eq? (string->symbol "X") 'x)  #f

(eq? (string->symbol "x")
     (string->symbol "x"))  #t

procedure: (symbol->string symbol)
returns: a string, the name of symbol

The string returned by symbol->string for a symbol created by an earlier call to string->symbol may or may not be the same string (by eq?) as the string passed to string->symbol. That is, an implementation is free to copy or not to copy a string it uses as the name of a symbol. Unpredictable behavior can result if a string passed to string->symbol is altered with string-set! or by any other means.

(symbol->string 'xyz)  "xyz"
(symbol->string (string->symbol "Hi"))  "Hi"
(symbol->string (string->symbol "()"))  "()"

R. Kent Dybvig / The Scheme Programming Language, Third Edition
Copyright © 2003 The MIT Press. Electronically reproduced by permission.
Illustrations © 2003 Jean-Pierre Hébert
ISBN 0-262-54148-3 / LOC QA76.73.S34D93
to order this book / about this book

http://www.scheme.com