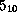, and
#36rZ is 
.
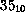This chapter describes Chez Scheme extensions to the standard set of operations on numbers. See Chapter 6 of The Scheme Programming Language, Second Edition or the Revised5 Report on Scheme for a description of standard operations on numbers.
Chez Scheme supports the full set of Scheme numeric datatypes, including exact and inexact integer, rational, real, and complex numbers. A variety of representations are used to support these datatypes:
Most numbers can be represented in only one way; however, real numbers are sometimes represented as inexact complex numbers with imaginary component equal to zero.
Chez Scheme extends the syntax of numbers with arbitrary radixes from two through 36, nondecimal floating-point and scientific notation, and printed representations for IEEE infinities and NANs. (NAN stands for "not-a-number.")
Arbitrary radixes are specified with the prefix #nr, where
n ranges from 2 through 36.
Digits beyond 9 are specified with the letters (in either
upper or lower case) a through z.
For example, #2r101 is 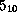, and
#36rZ is .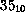
For higher radixes, an ambiguity arises between the interpretation of certain letters, e.g., e, as digits or exponent specifiers; in such cases, the letter is assumed to be a digit. For example, the e in #x3.2e5 is interpreted as a digit, not as an exponent marker, whereas in 3.2e5 it is treated as an exponent marker.
IEEE infinities are printed as +inf.0 and -inf.0, while IEEE NANs are printed as +nan.0 or -nan.0. (+nan.0 is used on output for all NANs.)
(/ 1.0 0.0) 
+inf.0
(/ 1.0 -0.0) -inf.0
(/ 0.0 0.0) +nan.0
(/ +inf.0 -inf.0) +nan.0
The first section of this chapter describes type-specific numeric type predicates. The next three sections describe fast, type-specific numeric operations on fixnums, flonums, and inexact complex numbers (flonums and/or inexact complexnums). The fixnum-specific versions should be used only when the programmer is certain that the operands and results (where appropriate) will be fixnums, i.e., integers in the range (most-negative-fixnum) to (most-positive-fixnum), inclusive. The flonum-specific versions should be used only when the inputs and outputs (where appropriate) are certain to be flonums. The mixed flonum/complexnum versions should be used only when the inputs are certain to be either flonums or inexact complexnums. Random number generation and miscellaneous numeric operations are covered in the last two sections of this chapter.
procedure: (fixnum? obj)
returns: #t if obj is a fixnum, otherwise #f
(fixnum? 0) #t
(fixnum? (most-positive-fixnum)) #t
(fixnum? (most-negative-fixnum)) #t
(fixnum? (* (most-positive-fixnum) 2)) #f
(fixnum? 3/4) #f
(fixnum? 'a) #f
procedure: (bignum? obj)
returns: #t if obj is a bignum, otherwise #f
(bignum? 0) #f
(bignum? (most-positive-fixnum)) #f
(bignum? (most-negative-fixnum)) #f
(bignum? (* (most-positive-fixnum) 2)) #t
(bignum? 3/4) #f
(bignum? 'a) #f
procedure: (ratnum? obj)
returns: #t if obj is a ratnum, otherwise #f
(ratnum? 0) #f
(ratnum? (* (most-positive-fixnum) 2)) #f
(ratnum? 3/4) #t
(ratnum? -10/2) #f
(ratnum? -11/2) #t
(ratnum? 'a) #f
procedure: (flonum? obj)
returns: #t if obj is a flonum, otherwise #f
(flonum? 0) #f
(flonum? 3/4) #f
(flonum? #i3/4) #t
(flonum? .02) #t
(flonum? 1e10) #t
(flonum? 3.0+0.0i) #f
procedure: (cflonum? obj)
returns: #t if obj is an inexact complexnum or flonum, otherwise #f
(cflonum? 0) #f
(cflonum? 0.0) #t
(cflonum? 3+4i) #f
(cflonum? 3.0+4i) #t
(cflonum? +i) #f
(cflonum? +1.0i) #t
At optimization levels 0, 1, and 2 the fixnum-specific procedures check their inputs and outputs (where appropriate), while at optimization level 3 the compiler generates, in most cases, code that does not perform these checks. Fixnum-specific procedure names begin with the prefix "fx" to set them apart from their generic counterparts. The remainder of this section describes the fixnum-specific procedures.
procedure: (most-positive-fixnum)
returns: the most positive fixnum supported by the system
The value returned by most-positive-fixnum determines the most positive value that is valid as input to or output from fixnum-only procedures.
procedure: (most-negative-fixnum)
returns: the most negative fixnum supported by the system
The value returned by most-negative-fixnum determines the most negative value that is valid as input to or output from fixnum-only procedures.
procedure: (fx= fixnum1 fixnum2 ...)
procedure: (fx< fixnum1 fixnum2 ...)
procedure: (fx> fixnum1 fixnum2 ...)
procedure: (fx<= fixnum1 fixnum2 ...)
procedure: (fx>= fixnum1 fixnum2 ...)
returns: #t if the relation holds, #f otherwise
The predicate fx= returns #t if its arguments are equal. The predicate fx< returns #t if its arguments are monotonically increasing, i.e., each argument is greater than the preceding ones, while fx> returns #t if its arguments are monotonically decreasing. The predicate fx<= returns #t if its arguments are monotonically nondecreasing, i.e., each argument is not less than the preceding ones, while fx>= returns #t if its arguments are monotonically nonincreasing. When passed only one argument, each of these predicates returns #t.
(fx= 0) #t
(fx= 0 0) #t
(fx< (most-negative-fixnum) 0 (most-positive-fixnum)) #t
(let ([x 3]) (fx<= 0 x 9)) #t
(fx<= 0 3 3) #t
(fx>= 0 0 (most-negative-fixnum)) #t
procedure: (fxzero? fixnum)
returns: #t if fixnum is zero, #f otherwise
fxzero? is equivalent to (lambda (x) (fx= x 0)).
(fxzero? 0) #t
(fxzero? 1) #f
procedure: (fxpositive? fixnum)
returns: #t if fixnum is greater than zero, #f otherwise
fxpositive? is equivalent to (lambda (x) (fx> x 0)).
(fxpositive? 128) #t
(fxpositive? 0) #f
(fxpositive? -1) #f
procedure: (fxnegative? fixnum)
returns: #t if fixnum is less than zero, #f otherwise
fxnegative? is equivalent to (lambda (x) (fx< x 0)).
(fxnegative? -65) #t
(fxnegative? 0) #f
(fxnegative? 1) #f
procedure: (fxnonpositive? fixnum)
returns: #t if fixnum is not greater than zero, #f otherwise
fxnonpositive? is equivalent to (lambda (x) (fx<= x 0)).
(fxnonpositive? 128) #f
(fxnonpositive? 0) #t
(fxnonpositive? -1) #t
procedure: (fxnonnegative? fixnum)
returns: #t if fixnum is not less than zero, #f otherwise
fxnonnegative? is equivalent to (lambda (x) (fx>= x 0)).
(fxnonnegative? -65) #f
(fxnonnegative? 0) #t
(fxnonnegative? 1) #t
procedure: (fxeven? fixnum)
returns: #t if fixnum is even, #f otherwise
(fxeven? 0) #t
(fxeven? 1) #f
(fxeven? -1) #f
(fxeven? -10) #t
procedure: (fxodd? fixnum)
returns: #t if fixnum is odd, #f otherwise
(fxodd? 0) #f
(fxodd? 1) #t
(fxodd? -1) #t
(fxodd? -10) #f
procedure: (fx+ fixnum ...)
returns: the sum of the arguments fixnum ...
When called with no arguments, fx+ returns 0.
(fx+) 0
(fx+ 1 2) 3
(fx+ 3 4 5) 12
(apply fx+ '(1 2 3 4 5)) 15
procedure: (fx- fixnum1 fixnum2 ...)
returns: a fixnum
When called with one argument, fx- returns the negative of fixnum1. Thus, (fx- fixnum1) is an idiom for (fx- 0 fixnum1).
When called with two or more arguments, fx- returns the result of subtracting the sum of the numbers fixnum2 ... from fixnum1.
(fx- 3) -3
(fx- 4 3) 1
(fx- 4 3 2 1) -2
procedure: (fx* fixnum ...)
returns: the product of the arguments fixnum ...
When called with no arguments, fx* returns 1.
(fx*) 1
(fx* 1 2) 2
(fx* 3 -4 5) -60
(apply fx* '(1 -2 3 -4 5)) 120
procedure: (fx/ fixnum1 fixnum2 ...)
returns: see explanation
When called with one argument, fx/ returns the reciprocal of fixnum1. That is, (fx/ fixnum1) is an idiom for (fx/ 1 fixnum1).
When called with two or more arguments, fx/ returns the result of dividing fixnum1 by the product of the remaining arguments fixnum2 ....
(fx/ 1) 1
(fx/ -17) 0
(fx/ 8 -2) -4
(fx/ -9 2) -4
(fx/ 60 5 3 2) 2
procedure: (fx1+ fixnum)
procedure: (fx1- fixnum)
returns: fixnum plus 1 or fixnum minus 1
(define fxplus
(lambda (x y)
(if (fxzero? x)
y
(fxplus (fx1- x) (fx1+ y)))))
(fxplus 7 8) 15
fx1+ and fx1- can be defined as follows:
(define fx1+ (lambda (x) (fx+ x 1)))
(define fx1- (lambda (x) (fx- x 1)))
procedure: (fxquotient fixnum1 fixnum2)
returns: see explanation
fxquotient is identical to fx/. See the description of fx/ above.
procedure: (fxremainder fixnum1 fixnum2)
returns: the fixnum remainder of fixnum1 divided by fixnum2
The result of fxremainder has the same sign as fixnum1.
(fxremainder 16 4) 0
(fxremainder 5 2) 1
(fxremainder -45 7) -3
(fxremainder 10 -3) 1
(fxremainder -17 -9) -8
procedure: (fxmodulo fixnum1 fixnum2)
returns: the fixnum modulus of fixnum1 and fixnum2
The result of fxmodulo has the same sign as fixnum2.
(fxmodulo 16 4) 0
(fxmodulo 5 2) 1
(fxmodulo -45 7) 4
(fxmodulo 10 -3) -2
(fxmodulo -17 -9) -8
procedure: (fxabs fixnum)
returns: the absolute value of fixnum
(fxabs 1) 1
(fxabs -1) 1
(fxabs 0) 0
procedure: (fxmax fixnum1 fixnum2 ...)
returns: the maximum of fixnum1 fixnum2 ...
(fxmax 4 -7 2 0 -6) 4
(let ([ls '(7 3 5 2 9 8)])
(apply fxmax ls)) 9
procedure: (fxmin fixnum1 fixnum2 ...)
returns: the minimum of fixnum1 fixnum2 ...
(fxmin 4 -7 2 0 -6) -7
(let ([ls '(7 3 5 2 9 8)])
(apply fxmin ls)) 2
procedure: (fxlogand fixnum1 fixnum2)
returns: the logical "and" of fixnum1 and fixnum2
The arguments are taken as two's complement integers, regardless of the underlying representation.
(fxlogand -1 -1) -1
(fxlogand -1 0) 0
(fxlogand 5 3) 1
procedure: (fxlogor fixnum1 fixnum2)
returns: the logical "or" of fixnum1 and fixnum2
The arguments are taken as two's complement integers, regardless of the underlying representation.
(fxlogor -1 -1) -1
(fxlogor -1 0) -1
(fxlogor 5 3) 7
procedure: (fxlogxor fixnum1 fixnum2)
returns: the logical "exclusive or" of fixnum1 and fixnum2
The arguments are taken as two's complement integers, regardless of the underlying representation.
(fxlogxor -1 -1) 0
(fxlogxor -1 0) -1
(fxlogxor 5 3) 6
procedure: (fxlognot fixnum)
returns: the logical "not" of fixnum
The argument is taken as a two's complement integer, regardless of the underlying representation.
(fxlognot -1) 0
(fxlognot 0) -1
procedure: (fxsll fixnum1 fixnum2)
returns: fixnum1 shifted left by fixnum2
The first argument is taken as two's complement integer, regardless of the underlying representation. The second argument must be nonnegative.
(fxsll 1 2) 4
(fxsll -1 2) -4
procedure: (fxsrl fixnum1 fixnum2)
returns: fixnum1 logically shifted right by fixnum2
The first argument is taken as two's complement integer, regardless of the underlying representation. The second argument must be nonnegative.
(fxsrl 4 2) 1
(= (fxsrl -1 1) (most-positive-fixnum)) #t
procedure: (fxsra fixnum1 fixnum2)
returns: fixnum1 arithmetically shifted right by fixnum2
The first argument is taken as two's complement integer, regardless of the underlying representation. The second argument must be nonnegative.
(fxsra 64 3) 8
(fxsra -1 1) -1
(fxsra -64 3) -8
Inexact real numbers are normally represented by flonums. A flonum is a single 64-bit double-precision floating point number. This section describes operations on flonums, most of which accept flonum arguments and return flonum values. In most cases, the operations are inline-coded or coded as machine language subroutines at optimize-level 3 with no argument type checking; full type checking is performed at lower optimize levels. Flonum-specific procedure names begin with the prefix "fl" to set them apart from their generic counterparts.
Inexact real numbers may also be represented by inexact complexnums with imaginary parts equal to zero, which cannot be used as input to the flonum-specific operators. Such numbers are produced, however, only from operations involving complex numbers with nonzero imaginary parts, by explicit calls to fl-make-rectangular, make-rectangular, or make-polar, or by numeric input in either polar or rectangular format.
procedure: (fixnum->flonum fixnum)
returns: the flonum representation for fixnum
fixnum->flonum is a restricted version of exact->inexact, which converts any numeric representation to its inexact equivalent if one exists.
(fixnum->flonum 0) 0.0
(fixnum->flonum 13) 13.0
procedure: (flonum->fixnum flonum)
returns: the fixnum representation of flonum, truncated
The truncated value of flonum must fall within the fixnum range. flonum->fixnum is a restricted version of inexact->exact, which converts any numeric representation to its exact equivalent.
(flonum->fixnum 0.0) 0
(flonum->fixnum 3.9) 3
(flonum->fixnum -2.2) -2
procedure: (fl= flonum1 flonum2 ...)
procedure: (fl< flonum1 flonum2 ...)
procedure: (fl> flonum1 flonum2 ...)
procedure: (fl<= flonum1 flonum2 ...)
procedure: (fl>= flonum1 flonum2 ...)
returns: #t if the relation holds, #f otherwise
The predicate fl= returns #t if its arguments are equal. The predicate fl< returns #t if its arguments are monotonically increasing, i.e., each argument is greater than the preceding ones, while fl> returns #t if its arguments are monotonically decreasing. The predicate fl<= returns #t if its arguments are monotonically nondecreasing, i.e., each argument is not less than the preceding ones, while fl>= returns #t if its arguments are monotonically nonincreasing. When passed only one argument, each of these predicates returns #t.
IEEE NANs are not comparable, i.e., comparisons involving NANs always return #f.
(fl= 0.0) #t
(fl= 0.0 0.0) #t
(fl< -1.0 0.0 1.0) #t
(fl> -1.0 0.0 1.0) #f
(fl<= 0.0 3.0 3.0) #t
(fl>= 4.0 3.0 3.0) #t
(fl< 7.0 +inf.0) #t
(fl= +nan.0 0.0) #f
(fl= +nan.0 +nan.0) #f
(fl< +nan.0 +nan.0) #f
(fl> +nan.0 +nan.0) #f
procedure: (fl+ flonum ...)
returns: the sum of the arguments flonum ...
When called with no arguments, fl+ returns 0.0.
(fl+) 0.0
(fl+ 1.0 2.0) 3.0
(fl+ 3.0 4.0 5.0) 12.0
(apply fl+ '(1.0 2.0 3.0 4.0 5.0)) 15.0
procedure: (fl- flonum1 flonum2 ...)
returns: see explanation
When called with one argument, fl- returns the negative of flonum1. When called with two or more arguments, fl- returns the result of subtracting the sum of the numbers flonum2 ... from flonum1.
fl- for one argument is equivalent to
(lambda (x) (fl* -1.0 x))
or
(lambda (x) (fl- -0.0 x))
but not
(lambda (x) (fl- 0.0 x))
since the latter returns 0.0 for 0.0.
(fl- 0.0) -0.0
(fl- 3.0) -3.0
(fl- 4.0 3.0) 1.0
(fl- 4.0 3.0 2.0 1.0) -2.0
procedure: (fl* flonum ...)
returns: the product of the arguments flonum ...
When called with no arguments, fl* returns 1.0.
(fl*) 1.0
(fl* 1.0 2.0) 2.0
(fl* 3.0 -4.0 5.0) -60.0
(apply fl* '(1.0 -2.0 3.0 -4.0 5.0)) 120.0
procedure: (fl/ flonum1 flonum2 ...)
returns: see explanation
When called with one argument, fl/ returns the reciprocal of flonum1. That is, (fl/ flonum1) is an idiom for (fl/ 1.0 flonum1).
When called with two or more arguments, fl/ returns the result of dividing flonum1 by the product of the remaining arguments flonum2 ....
(fl/ -4.0) -0.25
(fl/ 8.0 -2.0) -4.0
(fl/ -9.0 2.0) -4.5
(fl/ 60.0 5.0 3.0 2.0) 2.0
procedure: (flabs flonum)
returns: absolute value of flonum
flabs is a restricted version of abs or magnitude, which allow either argument to be any valid representation for a real number.
(flabs 3.2) 3.2
(flabs -2e-20) 2e-20
procedure: (decode-float x)
returns: see below
x must be a flonum. decode-float returns a vector with three integer elements, m, e, and s, such that x = sm2e. It is useful primarily in the printing of floating-point numbers.
(decode-float 1.0) #3(4503599627370496 -52 1)
(decode-float -1.0) #3(4503599627370496 -52 -1)
(define slow-identity
(lambda (x)
(exact->inexact
(let ((v (decode-float x)))
(let ((m (vector-ref v 0))
(e (vector-ref v 1))
(s (vector-ref v 2)))
(* s m (expt 2 e)))))))
(slow-identity 1.0) 1.0
(slow-identity -1e20) -1e20
procedure: (fllp flonum)
returns: see below
fllp returns the 12-bit integer consisting of the exponent plus highest order represented bit of a flonum (ieee 64-bit floating-point number). It can be used to compute a fast approximation of the logarithm of the number.
(fllp 0.0) 0
(fllp 1.0) 2046
(fllp -1.0) 2046
(fllp 1.5) 2047
(fllp +inf.0) 4094
(fllp -inf.0) 4094
(fllp #b1.0e-1111111111) 1
(fllp #b1.0e-10000000000) 0
The procedures described in this section provide mechanisms for creating and operating on inexact complex numbers. Inexact complex numbers with nonzero imaginary parts are represented as inexact complexnums. An inexact complexnum contains two 64-bit double-precision floating point numbers. Inexact complex numbers with imaginary parts equal to zero (in other words, inexact real numbers) may be represented as either inexact complexnums or flonums. The operations described in this section accept any mix of inexact complexnum and flonum arguments (collectively, "cflonums").
In most cases, the operations are performed with minimal type checking at optimize-level 3; full type checking is performed at lower optimize levels. Inexact complex procedure names begin with the prefix "cfl" to set them apart from their generic counterparts.
procedure: (fl-make-rectangular flonum1 flonum2)
returns: an inexact complexnum
The inexact complexnum produced by fl-make-rectangular has real part equal to flonum1 and imaginary part equal to flonum2.
(fl-make-rectangular 2.0 -3.0) 2.0-3.0i
(fl-make-rectangular 2.0 0.0) 2.0+0.0i
(fl-make-rectangular 2.0 -0.0) 2.0-0.0i
procedure: (cfl-real-part cflonum)
returns: the real part of cflonum
procedure: (cfl-imag-part cflonum)
returns: the imaginary part of cflonum
(cfl-real-part 2.0-3.0i) 2.0
(cfl-imag-part 2.0-3.0i) -3.0
(cfl-imag-part 2.0-0.0i) -0.0
(cfl-imag-part 2.0-inf.0i) -inf.0
procedure: (cfl= cflonum1 cflonum2)
returns: #t if cflonum1 is equal to cflonum2, #f otherwise
(cfl= 7.0+0.0i 7.0) #t
(cfl= 1.0+2.0i 1.0+2.0i) #t
(cfl= 1.0+2.0i 1.0-2.0i) #f
procedure: (cfl+ cflonum1 cflonum2)
procedure: (cfl- cflonum1 cflonum2)
procedure: (cfl* cflonum1 cflonum2)
procedure: (cfl/ cflonum1 cflonum2)
returns: a cflonum
These procedures compute the sum, difference, product, or quotient of inexact complex quantities, whether these quantities are represented by flonums or inexact complexnums. For example, if cfl+ receives two flonum arguments a and b, it returns the sum a + b; in this case, it behaves the same as fl+. With two inexact complexnum arguments a + bi and c + di, it returns the sum (a + c) + (b + d)i. If one argument is a flonum a and the other an inexact complexnum c + di, cfl+ returns (a + c) + di.
(cfl+ 1.0+2.2i -3.7+5.3i) -2.7+7.5i
(cfl+ 1.0 -5.3) -4.3
(cfl+ 1.0 -5.3i) 1.0-5.3i
(cfl- 1.0+2.5i -3.7) 4.7+2.5i
(cfl* 1.0+2.0i 3.0+4.0i) -5.0+10.0i
(cfl/ -5.0+10.0i 1.0+2.0i) 3.0+4.0i
procedure: (cfl-conjugate cflonum)
returns: complex conjugate of cflonum
The procedure cfl-conjugate, when passed an inexact complex argument a + bi, returns its complex conjugate a + (-b)i.
See also conjugate, which is a generic version of this operator that returns the complex conjugate of any valid representation for a complex number.
(cfl-conjugate 3.0) 3.0
(cfl-conjugate 3.0+4.0i) 3.0-4.0i
(cfl-conjugate 1e-20-2e-30i) 1e-20+2e-30i
procedure: (cfl-magnitude-squared cflonum)
returns: magnitude of cflonum squared
The procedure cfl-magnitude-squared, when passed an inexact complex argument a + bi returns a flonum representing the magnitude of the argument squared, i.e., a2 + b2.
See also magnitude-squared, which is a generic version of this operator that returns the magnitude squared of any valid representation for a complex number. Both operations are similar to the magnitude procedure, which returns the magnitude, sqrt(a2 + b2), of its generic complex argument.
(cfl-magnitude-squared 3.0) 9.0
(cfl-magnitude-squared 3.0-4.0i) 25.0
procedure: (random real)
returns: a nonnegative pseudo-random number less than real
real must be a positive integer or positive inexact real number.
(random 1) 0
(random 1029384535235) 1029384535001, every now and then
(random 1.0) 0.5, every now and then
The random number generator allows the current random seed to be obtained and modified via the parameter random-seed. The random seed should be set only to a previous value from random-seed to ensure proper operation of the random number generator.
(let ([s (random-seed)])
(let ([r1 (random 1.0)])
(random-seed s)
(eqv? (random 1.0) r1))) #t
procedure: (1+ num)
procedure: (add1 num)
procedure: (1- num)
procedure: (sub1 num)
returns: num plus 1 or num minus 1
1+ and add1 are equivalent to (lambda (x) (+ x 1)); 1- and sub1 are equivalent to (lambda (x) (- x 1)).
(define plus
; x should be a nonnegative integer
(lambda (x y)
(if (zero? x)
y
(plus (1- x) (1+ y)))))
(plus 7 8) 15
(define double
; x should be a nonnegative integer
(lambda (x)
(if (zero? x)
0
(add1 (add1 (double (sub1 x)))))))
(double 7) 14
procedure: (expt-mod int1 int2 int3)
returns: int1 raised to the int2 power, modulo int3
int1, int2 and int3 must be nonnegative integers. expt-mod performs its computation in such a way that the intermediate results are never much larger than int3. This means that when int2 is large, expt-mod is more efficient than the equivalent procedure (lambda (x y z) (modulo (expt x y) z)).
(expt-mod 2 4 3) 1
(expt-mod 2 76543 76543) 2
procedure: (isqrt n)
returns: the integer square root of n
n must be a nonnegative integer.
The integer square root of n is defined to be
.
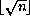(isqrt 0) 0
(isqrt 16) 4
(isqrt 16.0) 4.0
(isqrt 20) 4
(isqrt 20.0) 4.0
(isqrt (* 2 (expt 10 20))) 14142135623
procedure: (integer-length n)
returns: see below
The procedure integer-length returns the length in bits of the smallest two's complement representation for n, with an assumed leading 1 (sign) bit for negative numbers. For zero, integer-length returns 0.
(integer-length 0) 0
(integer-length 1) 1
(integer-length 2) 2
(integer-length 3) 2
(integer-length 4) 3
(integer-length #b10000000) 8
(integer-length #b11111111) 8
(integer-length -1) 0
(integer-length -2) 1
(integer-length -3) 2
(integer-length -4) 2
procedure: (ash n m)
returns: n shifted left arithmetically by m.
Both arguments must be exact integers. The first argument is taken as a two's complement integer, regardless of the underlying representation. If m is negative, n is shifted right by -m bits.
(ash 8 0) 8
(ash 8 2) 32
(ash 8 -2) 2
(ash -1 2) -4
(ash -1 -2) -1
procedure: (nonpositive? real)
returns: #t if real is not greater than zero, #f otherwise
nonpositive? is equivalent to (lambda (x) (<= x 0)).
(nonpositive? 128) #f
(nonpositive? 0.0) #t
(nonpositive? 1.8e-15) #f
(nonpositive? -2/3) #t
procedure: (nonnegative? real)
returns: #t if real is not less than zero, #f otherwise
nonnegative? is equivalent to (lambda (x) (>= x 0)).
(nonnegative? -65) #t
(nonnegative? 0) #t
(nonnegative? -0.0121) #f
(nonnegative? 15/16) #t
procedure: (conjugate number)
returns: complex conjugate of number
The procedure conjugate, when passed a complex argument a + bi, returns its complex conjugate a + (-b)i.
(conjugate 3.0+4.0i) 3.0-4.0i
(conjugate 1e-20-2e-30i) 1e-20+2e-30i
(conjugate 3) 3
procedure: (magnitude-squared number)
returns: magnitude of number squared
The procedure magnitude-squared, when passed a complex argument a + bi returns its magnitude squared, i.e., a2 + b2.
(magnitude-squared 3.0-4.0i) 25.0
(magnitude-squared 3.0) 9.0
procedure: (sinh num)
procedure: (cosh num)
procedure: (tanh num)
returns: the hyperbolic sine, cosine, or tangent of num
(sinh 0.0) 0.0
(cosh 0.0) 1.0
(tanh -0.0) -0.0
procedure: (asinh num)
procedure: (acosh num)
procedure: (atanh num)
returns: the hyperbolic arc sine, arc cosine, or arc tangent of num
(acosh 0.0) 0.0+1.5707963267948966i
(acosh 1.0) 0.0
(atanh -1.0) -inf.0
 |
Chez Scheme User's Guide © 1998 R. Kent Dybvig Cadence Research Systems http://www.scheme.com Illustrations © 1998 Jean-Pierre Hébert about this book |