
Chapter 12. Compatibility Features
This chapter describes several items that are included with current
versions of Chez Scheme primarily for compatibility with older
versions of the system.
The first two sections describe expansion-passing-style and
extend-syntax macros.
These features are supported directly by current versions of Chez Scheme,
but support may be dropped in future versions.
New programs should use the syntax-case facility described in
The Scheme Programming Language, Second Edition [9]
instead.
The third section describes a compatibility file distributed with
Chez Scheme that contains definitions for forms and procedures no
longer supported directly by Chez Scheme.
Section 12.1. Expansion-Passing-Style Macros
Earlier versions of Chez Scheme provided two complimentary macro
systems: a low-level
"expansion-passing-style" (EPS) macro system
and a high-level
extend-syntax system.
The extend-syntax system was defined in terms of the lower-level
system.
extend-syntax is also supported, to a limited degree, by the
syntax-case system.
While it is not possible to intermix macros written using
expansion-passing-style
macros with syntax-case macros, it is possible to
enable the EPS expander,
allowing existing programs to be run without the need to rewrite macro
definitions.
The expander used by the compiler, interpreter, and direct calls to
expand is determined by the value
of the parameter current-expand.
Its default value is sc-expand, the syntax-case
expander.
It must be set to eps-expand to
enable support for expansion-passing-style macros.
An EPS macro is a procedure, or expander, associated with a keyword,
that accepts two arguments: the expression to expand and an expander
with which to perform further expansion.
The expander associated with a keyword may choose to apply the
expander passed to it to the entire expression it builds before
returning, it may choose to apply the expander to selected pieces
of the expression it builds, or it may choose not to use the
expander.
It may even use a different expander from the one given to it
to expand the expression or pieces of the expression it builds.
Expansion-passing style is described fully in the article
"Expansion-passing style: a general macro
mechanism" [12].
EPS macros are defined using the procedure install-expander or
the syntactic form define-syntax-expander.
procedure: (install-expander keyword expander)
returns: unspecified
keyword must be a symbol, and
expander must be a procedure.
install-expander associates expander with the keyword
keyword for purposes of macro expansion.
When the expander (see eps-expand and
eps-expand-once) finds a
list-structured expression whose car is keyword, expander
is passed the expression and an expander with which to perform
further expansion.
New programs should employ syntax-case instead.
syntax: (define-syntax-expander keyword exp)
returns: unspecified
keyword must be a symbol, and
exp must evaluate to a procedure.
define-syntax-expander associates the expansion procedure (expander)
obtained by evaluating exp with the keyword
keyword for purposes of macro expansion.
When the expander (see eps-expand
and eps-expand-once) finds a
list-structured expression whose car is keyword, the expander
is passed the expression and an expander with which to perform
further expansion.
define-syntax-expander differs from install-expander in two ways:
First, the keyword expression keyword is not evaluated.
Second, a define-syntax-expander form is implicitly wrapped
in an eval-when expression with all three options
(compile, load, and eval) specified, so that syntax expander
definitions appearing within a file are available to subsequent
expressions in the file when the file is processed by compile-file.
extend-syntax
is layered on top of define-syntax-expander, as
can be seen by applying
eps-expand-once
to an extend-syntax form.
New programs should employ syntax-case instead.
(define-syntax-expander quote
(lambda (x e)
x))
(define-syntax-expander let*
; no syntax checking (should be written with extend-syntax!)
(lambda (x e)
(let ([bindings (cadr x)] [exps (cddr x)])
(if (null? bindings)
(e `(let () ,@exps) e)
(e `(let (,(car bindings))
(let* ,(cdr bindings) ,@exps)) e)))))
(eps-expand-once '(quote a)) 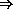 (quote a)
(quote a)
(eps-expand-once
'(let* ([x 'a] [y x]) y)) 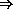 (let ([x 'a]) (let* ([y x]) y))
(let ([x 'a]) (let* ([y x]) y))
Section 12.2. Extend-Syntax Macros
This section describes extend-syntax, a powerful yet easy to use
syntactic extension facility based on
pattern matching [21].
Syntactic transformations written using
extend-syntax are similar to those written using a
define-syntax with syntax-case, except that the
transformations produced by extend-syntax do not automatically
respect lexical scoping.
extend-syntax is supported by the syntax-case
expander as well as by the EPS expander.
It is not always possible, however, to mix syntactic abstractions
written using syntax-case with those written using
extend-syntax; it is generally preferable to use one or the
other wherever possible.
Support for extend-syntax within the syntax-case expander
is provided only as an aid to migrating to syntax-case.
syntax: (extend-syntax (name key ...) (pat fender template) ...)
returns: unspecified
The identifier name is the name, or syntax keyword, for the
syntactic extension to be defined.
When the system expander processes any list expression whose car is
name, the syntactic transformation procedure generated by
extend-syntax is invoked on this expression.
The remaining identifiers key ... are additional keywords to
be recognized within input expressions during expansion (such as
else in cond or case).
Each clause after the list of keys consists of a pattern pat, an
optional fender,
and a template.
The optional fender is omitted more often than not.
The pat specifies the syntax the input expression must have
for the clause to be chosen.
Identifiers within the pattern that are not keywords
(pattern variables) are bound to corresponding pieces of the input expression.
If present, the fender is a Scheme expression that specifies
additional constraints on the input expression (accessed through the
pattern variables) that must be satisfied in order for the clause to
be chosen.
The template specifies what form the output takes, usually in
terms of the pattern variables.
During expansion, the transformation procedure extend-syntax
generates attempts to match the input expression against each
pattern in the order the clauses are given.
If the input expression matches the pattern, the pattern variables are
bound to the corresponding pieces of the input expression and the
fender for the clause, if any, is evaluated.
If the fender returns a true value, the given expansion is performed.
If input does not match the pattern or if the fender returns a false
value, the transformation procedure tries the next clause.
An error is signaled if no clause can be chosen.
Within the pattern,
ellipsis
(...) may be
used to specify zero or more occurrences
of the preceding pattern fragment, or prototype.
Similarly, ellipses may be used in the output to specify the construction
of zero or more expansion prototypes.
In this case, the expansion prototype must contain part of an input pattern
prototype.
The use of patterns, templates, ellipses within patterns and templates,
and fenders is illustrated in the following sequence of examples.
The first example, defining rec, uses a single keyword, a single
clause with no fender, and no ellipses.
The call to eps-expand-once in this example and the ones that
follow assumes that the EPS expander has been enabled prior to the
use of extend-syntax using (current-expand eps-expand).
(extend-syntax (rec)
[(rec id val)
(let ([id #f])
(set! id val)
id)])
(eps-expand-once  (let ([eternal #f])
(let ([eternal #f])
'(rec eternal 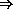 (set! eternal
(set! eternal
(lambda ()  (lambda ()
(lambda ()
(eternal))))  (eternal)))
(eternal)))
 eternal)
eternal)
The second example, defining when, shows
the use of ellipses.
(extend-syntax (when)
[(when test exp1 exp2 ...)
(if test (begin exp1 exp2 ...) #f)])
(eps-expand-once  (if (eq? msg 'print)
(if (eq? msg 'print)
'(when (eq? msg 'print) 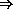 (begin (display "hi")
(begin (display "hi")
(display "hi")  (newline))
(newline))
(newline)))  #f)
#f)
The next example shows the definition of
let.
The definition of let shows the use of multiple ellipses, employing
one for the identifier/value pairs and one for the expressions in the body.
It also shows that the prototype need not be a single identifier, and that
pieces of the prototype may be separated from one another in the template.
(extend-syntax (let)
[(let ([x v] ...) e1 e2 ...)
((lambda (x ...) e1 e2 ...) v ...)])
(eps-expand-once  ((lambda (x y) (+ x y))
((lambda (x y) (+ x y))
'(let ([x 3] [y 4]) 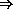 3
3
(+ x y)))  4)
4)
The next example shows let*, whose syntax is the same as for
let, but which is defined recursively in terms of let with
two clauses (one for the base case, one for the recursion step) since
it must produce a nested structure.
(extend-syntax (let*)
[(let* () e1 e2 ...)
(let () e1 e2 ...)]
[(let* ([x v] more ...) e1 e2 ...)
(let ([x v]) (let* (more ...) e1 e2 ...))])
The first pattern/template pair matches any let* expression with no
identifier/value pairs and maps it into the equivalent begin expression.
This is the base case.
The second pattern/template pair matches any let* expression with one
or more identifier/value pairs and transforms it into a let expression
binding the first pair whose body is a let* expression binding the
remaining pairs.
This is the recursion step, which will eventually lead us to the base case
because we remove one identifier/value pair at each step.
Notice that the second pattern uses the pattern variable more for the
second and later identifier/value pairs; this makes the pattern and template
less cluttered and makes it clear that only the first identifier/value pair
is dealt with explicitly.
It is interesting to try both eps-expand-once and
expand on a let* expression.
eps-expand-once shows the intermediate form in terms of let and
a simpler let* expression; expand shows the expression
completely expanded into applications of lambda expressions.
(eps-expand-once  (let ([x 3])
(let ([x 3])
'(let* ([x 3] [y x]) 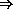 (let* ([y x])
(let* ([y x])
(+ x y)))  (+ x y)))
(+ x y)))
(expand  ((lambda (x)
((lambda (x)
'(let* ([x 3] [y x]) 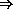 ((lambda (y) (+ x y)) x))
((lambda (y) (+ x y)) x))
(+ x y)))  3)
3)
The definition for and requires three clauses.
The first clause is necessary to recognize (and), and the second
two define all other and forms recursively.
(extend-syntax (and)
[(and) #t]
[(and x) x]
[(and x y ...) (if x (and y ...) #f)])
The definition for cond requires four clauses.
As with let*, cond must be described recursively, partly because
it produces nested if expressions, and partly because one
ellipsis prototype would not be sufficient to describe all possible
cond clauses.
The definition of cond also requires that we specify else as a
keyword, in addition to cond.
Here is the definition:
(extend-syntax (cond else)
[(cond) #f]
[(cond (else e1 e2 ...))
(begin e1 e2 ...)]
[(cond (test) more ...)
(or test (cond more ...))]
[(cond (test e1 e2 ...) more ...)
(if test
(begin e1 e2 ...)
(cond more ...))])
Two of the clauses are base cases and two are recursion steps.
The first base case is an empty cond.
The value of cond in this case is unspecified, so the choice of
#f is somewhat arbitrary.
The second base case is a cond containing only an else clause;
this is transformed to the equivalent begin expression.
The two recursion steps differ in the number of expressions in the cond
clause.
The value of cond when the first true clause contains only the test
expression is the value of the test.
This is similar to what or does, so we expand the cond clause
into an or expression.
On the other hand, when there are expressions following the test expression,
the value of the last expression is returned, so we use if and
begin.
(eps-expand-once  (if test
(if test
'(cond 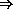 (begin exp1 exp2)
(begin exp1 exp2)
[test exp1 exp2]))  (cond))
(cond))
(eps-expand-once
'(cond [test])) 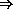 (or test (cond))
(or test (cond))
(expand  (if test1
(if test1
'(cond  exp1
exp1
[test1 exp1] 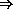 (if test2
(if test2
[test2 exp2]  exp2
exp2
[else exp3]))  exp3))
exp3))
To be absolutely correct about the syntax of let, we actually
must require that the bound identifiers in the input are symbols.
If we typed something like (let ([3 x]) x) we would not get an
error from let because it does not check to verify that the
objects in the identifier positions are symbols.
Instead, lambda may complain, or perhaps the system evaluator
long after expansion is complete.
This is where fenders
are useful.
(extend-syntax (let)
[(let ([x v] ...) e1 e2 ...)
(andmap symbol? '(x ...))
((lambda (x ...) e1 e2 ...) v ...)])
The andmap of symbol?
over '(x ...) assures that each
bound identifier is a symbol.
A fender is simply a Scheme expression.
Within that expression, any quoted object is first expanded by the same
rules as the template part of the clause.
In this case, '(x ...) is expanded to the list of identifiers from
the identifier/value pairs.
extend-syntax typically handles everything you need it for, but
some syntactic extension definitions require the ability to include the
result of evaluating an arbitrary Scheme expression.
This ability is provided by with.
syntax: (with ((pat exp) ...) template)
returns: processed template
with is valid only within an template inside of extend-syntax.
with patterns are the same as extend-syntax patterns, with
expressions are the same as extend-syntax fenders, and with
templates are the same as extend-syntax templates.
with can be used to introduce new pattern identifiers bound to
expressions produced by arbitrary Scheme expressions within
extend-syntax templates.
That is, with allows an escape from the declarative style of
extend-syntax into the procedural style of full Scheme.
One common use of with is the introduction of a temporary
identifier or list of temporary identifiers into a template.
with is also used to perform complex transformations that might
be clumsy or inefficient if performed within the extend-syntax
framework.
For example, or requires the use of a temporary identifier.
We could define or as follows.
(extend-syntax (or)
[(or) #f]
[(or x) x]
[(or x y ...)
(let ([temp x])
(if temp temp (or y ...)))])
This would work until we placed an or expression within the scope
of an occurrence of temp, in which case strange things could happen,
since extend-syntax does not respect lexical scoping.
(This is one of the reasons that define-syntax is preferable to
extend-syntax.)
(let ([temp #t])
(or #f temp)) 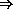 #f
#f
One solution is to use
gensym and with to
create a temporary identifier, as follows.
(extend-syntax (or)
[(or) #f]
[(or x) x]
[(or x y ...)
(with ([temp (gensym)])
(let ([temp x])
(if temp temp (or y ...))))])
Also, with can be used to combine elements of the input pattern
in ways not possible directly with extend-syntax, such as the
following folding-plus example.
(extend-syntax (folding-plus)
[(folding-plus x y)
(and (number? 'x) (number? 'y))
(with ([val (+ 'x 'y)])
val)]
[(folding-plus x y) (+ x y)])
folding-plus collapses into the value of (+ x y) if both
x and y are numeric constants.
Otherwise, folding-plus is transformed into (+ x y) for
later evaluation.
The fender checks that the operands are numbers at expansion time, and
the with performs the evaluation.
As with fenders, expansion is performed only within a quoted expressions,
since quote sets the data apart from the remainder of the Scheme
expression.
(eps-expand-once '(folding-plus 3 4.3)) 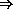 7.3
7.3
(eps-expand-once '(folding-plus 3 x)) 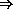 (+ 3 x)
(+ 3 x)
The example below binds a list of pattern variables to a list of
temporary symbols, taking advantage of the fact that with allows
us to bind patterns to expressions.
This list of temporaries helps us to implement the sigma syntactic
extension.
sigma is similar to lambda, except it assigns the identifiers
in the identifier list instead of creating new bindings.
It may be used to perform a series of assignments in parallel.
(extend-syntax (sigma)
[(sigma (x ...) e1 e2 ...)
(with ([(t ...) (map (lambda (x) (gensym)) '(x ...))])
(lambda (t ...)
(set! x t) ...
e1 e2 ...))])
(eps-expand-once  (lambda (G0 G1)
(lambda (G0 G1)
'(sigma (x y) 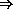 (set! x G0)
(set! x G0)
(list x y)))  (set! y G1)
(set! y G1)
 (list x y))
(list x y))
(let ([x 'a] [y 'b])
((sigma (x y) (list x y)) y x)) 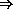 (b a)
(b a)
The final example below uses extend-syntax to implement
define-structure, following a similar example using
syntax-case in The Scheme Programming Language, Second
Edition.
The definition of define-structure makes use of two pattern/template
clauses.
Two clauses are needed to handle the optionality of the second subexpression.
The first clause matches the form without the second subexpression and
merely converts it into the equivalent form with the second subexpression
present, but empty.
The definition also makes heavy use of with to evaluate Scheme
expressions at expansion time.
The first four with clauses are used to manufacture the identifiers
that name the automatically defined procedures.
(The procedure format is particularly useful here, but it could be
replaced with string-append!, using symbol->string as needed.)
The first two clauses yield single identifiers (for the constructor and
predicate), while the next two yield lists of identifiers (for the field
access and assignment procedures).
The fifth with clause (the final clause in the outer with)
is used to count the total length vector needed for each instance of
the structure, which must include room for the name and all of the fields.
The final with clause (the only clause in the inner with)
is used to create a list of vector indexes, one for each field (starting at
1, since the structure name occupies position 0).
(extend-syntax (define-structure)
[(define-structure (name id1 ...))
(define-structure (name id1 ...) ())]
[(define-structure (name id1 ...) ([id2 val] ...))
(with ([constructor
(string->symbol (format "make-~a" 'name))]
[predicate
(string->symbol (format "~a?" 'name))]
[(access ...)
(map (lambda (x)
(string->symbol
(format "~a-~a" 'name x)))
'(id1 ... id2 ...))]
[(assign ...)
(map (lambda (x)
(string->symbol
(format "set-~a-~a!" 'name x)))
'(id1 ... id2 ...))]
[count (length '(name id1 ... id2 ...))])
(with ([(index ...)
(let f ([i 1])
(if (= i 'count)
'()
(cons i (f (+ i 1)))))])
(begin
(define constructor
(lambda (id1 ...)
(let* ([id2 val] ...)
(vector 'name id1 ... id2 ...))))
(define predicate
(lambda (obj)
(and (vector? obj)
(= (vector-length obj) count)
(eq? (vector-ref obj 0) 'name))))
(define access
(lambda (obj)
(vector-ref obj index)))
...
(define assign
(lambda (obj newval)
(vector-set! obj index newval)))
...)))])
Section 12.3. Compatibility File
Current versions of Chez Scheme are distributed with a compatibility
file containing definitions of various syntactic forms and procedures
supported by earlier versions of Chez Scheme for which support has
since been dropped.
This file, examples/compat.ss, is typically installed in
/usr/local/lib/scheme on Unix systems.
In some cases, the forms and procedures found in compat.ss
have been dropped because they were infrequently used and easily
written directly in Scheme.
In other cases, the forms and procedures have been rendered obsolete by
improvements in the system.
In such cases, new code should be written to use the newer features,
and older code should be rewritten if possible to use the newer
features as well.
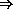 (quote a)
(quote a)
 (let ([x 'a]) (let* ([y x]) y))
(let ([x 'a]) (let* ([y x]) y))

 (let ([eternal #f])
(let ([eternal #f])